An Analytical Method for Predicting Temperature Rise Due to Multi-body Thermal Interaction in Deformation Processing

Abstract

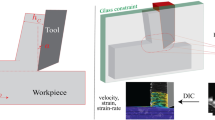
Thermal effects play a central role in determining the microstructure and mechanical properties during deformation processing. Unlike in directed energy processes, such as laser cladding or welding, prediction of temperature fields in deformation processing requires consideration of multiscale heat generation and heat transfer phenomena between the tool, workpiece, and surrounding lubricant. In this work, we develop an analytical method to evaluate the temperature rise in a workpiece as it interacts simultaneously with a tool and lubricant. The method operates on multiple length scales and partitions the generated heat using suitable temperature-matching principles. We demonstrate the utility of the scheme by analyzing two deformation processing operations—surface grinding and friction stir processing—and a problem in four-body wear, and compare the results with infrared thermography measurements. Final temperature predictions match well with experimentally measured values. Given its analytical nature, our scheme enables easy evaluation of parametric effects, thus distinguishing it from commonly used finite element techniques.

Appendix A Some Standard Temperature Models

The starting point for solutions of the 3D heat conduction equation is the corresponding Green’s function, defined as the steady state temperature distribution in a moving half-space (velocity V along the x-direction) when its surface heated by a continuous point source of strength $\tilde{q}$ (in watts) at the origin of coordinates:

$$ T_{{ss}} = \frac{{\tilde{q}}}{{2\pi K}}\left( {\frac{1}{r}} \right)\exp \left( { - \frac{V}{{2\alpha }}(r - x)} \right) $$

(17)

where $\alpha , K$ are the thermal diffusivity and conductivity of the material. Alternatively, the heat flux per unit time $\tilde{q}$may also be assumed to act at the point $(x^\prime ,y^\prime ,0)$ instead of origin, in which case (x,y) must be replaced by $(x-x^\prime )$ and $(y-y^\prime )$, respectively. Additionally, when the source is distributed over an area, one can appeal to linear superposition to write down the temperature distribution as:

$$ T(x,y,z) = \frac{1}{{2\pi K}}\int {\int {\frac{{\hat{q}{\text{d}}x^{\prime}{\text{d}}y^{\prime}}}{s}} } \exp \left( { - \frac{V}{{2\alpha }}(s - (x - x^{\prime}))} \right) $$

(18)

where $s=\sqrt{(x-x')^2+(y-y')^2+z^2}$ and $\hat{q}$ is now the heat intensity (W/m$^2$). Now, depending on the nature of heat distribution we can employ a suitable distribution for $\hat{q}$ and solve the integral in Eq. 18 to obtain temperatures in the material half-space. Three distributions are commonly employed [20]:

• 1. Uniform square distribution, where $\hat{q}(x^\prime ,y^\prime ) = \hat{q}_0 = \text {constant}$ and distributed over a square of side l, so that Eq. 18 can be integrated over non-dimensionalized variables. The equivalent temperature rise (non-dimensionalized) can be computed as:

  $$ \begin{aligned} & \theta \left({\frac{x}{l},\frac{y}{l},\frac{z}{l}} \right) \\ & \quad = \frac{{TK}}{{\hat{q}l}} = \frac{1}{{2\pi }}\int_{{ - 1}}^{1} {\int_{{ - 1}}^{1} {\frac{{\exp ( - Pe(\sqrt {\xi ^{\prime 2} + \eta ^{\prime 2} } - \xi ^{\prime}))}}{{\sqrt {\xi ^{\prime 2} + \eta ^{\prime 2} } }}} } {\text{d}}\xi ^{\prime}{\text{d}}\eta ^{\prime} \\ \end{aligned} $$

  (19)

  where $\eta =\dfrac{y'}{l}$. The non-dimensional Peclet number $Pe = Vl/2\alpha$ is a measure of how quickly the heat is being conducted away by the moving workpiece. For various Pe, this integral can be solved using simple numerical techniques to obtain the steady-state temperature distribution in the workpiece.

• 2. Uniform circular distribution: If $\hat{q}= \hat{q}_0$ as before, but acts on a circular area of radius R, we convert the integral in Eq. 18 to angular coordinates $\psi , s$, with $\psi$ varying from 0 to $\pi$. The resulting integral can again be evaluated in non-dimensional form, with the resultant (non-dimensional) temperature distribution.

  $$ \begin{aligned} & \theta \left( {\frac{x}{l},\frac{y}{l},\frac{z}{l}} \right) \\ & = \frac{{TK}}{{\hat{q}l}} = \frac{1}{{4\pi }}\int_{0}^{\pi } {} \\ & \frac{{[\exp ( - Pe[\sqrt {1 - \xi ^{2} \sin ^{2} \psi } + \xi \cos \psi ](1 - \cos \psi )) - 1]}}{{Pe(1 - \cos \psi )}}d\psi \\ \end{aligned} $$

  (20)

  where $Pe=\frac{V R}{2 \alpha }$ is again the Peclet number and $\xi =r/R$. This expression can be integrated using a simple numerical scheme to obtain the final temperature distribution.

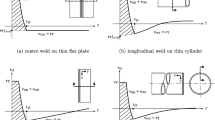
• 3. Continuous strip/band source: Instead of the square or circular sources, one often has to make an approximation that the source is infinite in one dimension. This is the case, for instance, when the width of the workpiece is much larger than the depth of interaction with the tool. For such situations, Eq. 18 may first be integrated with respect to $y^\prime$ from 0 to $\infty$ resulting in a line heat source. These may then be superimposed along the $x^\prime$ direction to obtain temperature distribution for a strip heat source

  $$ \begin{aligned} & T(x,y,z) \\ & = \int_{{ - l}}^{{ + l}} {\frac{{\bar{q}(x^{\prime } )}}{{\pi K}}} \exp \left( {\frac{{V(x - x^{\prime})}}{{2\alpha }}} \right) \\ & \quad \times K_{0} \left( {\frac{{V|x - x^{\prime}|}}{{2\alpha }}} \right)dx^{\prime} \\ \end{aligned} $$

  (21)

  where now $\bar{q}$ is the heat intensity per unit length (W/m) of a band heat source that is infinite along y axis and distributed along the x-axis; $K_0$ is the modified Bessel function of second kind of 0th order.