Design of phononic crystal using open resonators as harmful gases sensor

Abstract

This paper investigates the ability to use a finite one-dimensional phononic crystal composed of branched open resonators with a horizontal defect to detect the concentration of harmful gases such as CO₂. This research investigates the impact of periodic open resonators, defect duct at the center of the structure, and geometrical parameters such as cross-sections and length of the primary waveguide and resonators on the model's performance. As far as we know, this research is unique in the sensing field. Furthermore, these simulations show that the investigated finite one-dimensional phononic crystal composed of branched open resonators with a horizontal defect is a promising sensor.

Introduction

Massively producing pollutants in the air has threatened human health, the environment, and global biological ecosystems in recent years^1,2. So, detecting harmful gases to human health, such as CO₂, NO₂, NH₃, etc., piqued people's interest in protecting humans and the environment^3,4,5,6. As a result, numerous optical studies have been done on detecting toxic gaseous using two-dimension nanostructured materials, such as porous materials^5,7 and graphene^8,9. In addition, fluorescent, chemical, electrochemical, photonic crystal, and mass-sensitive are common gas sensors^10,11,12,13.

Phononic crystals (PnCs) are periodic artificial materials^14,15,16. PnCs have sparked considerable interest in various biosensing and chemical applications. PnCs can confine acoustic or elastic waves by creating stop frequency bands or phononic bandgaps (PnBGs) to propagate through them^17,18. Acoustic properties of materials, such as viscosity, density, speed of sound, elastic moduli, etc., can be probed by propagating the acoustic wave inside¹⁹. One-dimensional PnC (1D-PnC) sensors are resonant detectors. The main operating concept of 1D-PnC sensors is the multiple Bragg scattering of acoustic waves at each interface between two mediums with different acoustic impedance to produce a standing wave. The frequency of the PnBG depends on the traveling wave's acoustic speed and the structure's geometrical dimensions. Most 1D-PnC sensors are based on breaking the periodicity at the center of the structure, resulting in a resonant peak inside the PnBG. Adding this defect at the center of the structure confines a specific frequency called resonant frequency.

In traditional PnCs, continuity of flux and pressure are considered along the main direction of propagation. Recently, locally resonant elements have attracted attention in the field of periodic structures. However, lateral elements or resonators that depend on the change of pressure or flux stability in other paths can be added. These lateral elements can be closed or open ducts. In 2008, El Boudouti et al.²⁰ proposed a structure of a slender tube with lateral ducts. The presence of lateral tubes causes the formation of stop bands in the transmittance spectrum. In 2020, Antraoui et al. designed a periodic structure composed of a main duct with open resonators. But utilizing these structures with lateral resonators in gas sensing applications is still lacking.

Recently, gas sensors using PnCs attracted attention due to their advantages. For example, gas sensors using PnCs do not require a recovery time. Besides, as PnC doesn’t contain any electronic component, gas sensors using PnCs can give good measurements in complex environments such as in an explosive environment²¹. Furthermore, the low cost and ease of fabrication of PnC sensors are good advantages²².

As far as we know, this research is unique in the gas sensing field. Using branched open resonators enhanced the sensor's performance. Furthermore, these simulations show that the investigated finite one-dimensional phononic crystal composed of branched open resonators with a horizontal defect is a promising sensor. Furthermore, the proposed PnC sensor with branched open resonators can be easily fabricated using low-cost conventional materials.

Sensor configuration and equations

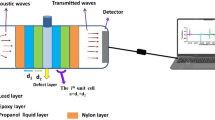
In Fig. 1, a schematic of the 1D-PnC composed of branched open resonators is proposed. The main guide has a cross-section S₁ and a thickness d₁. The branched open resonators have cross-section S₂ and height d₂. The proposed 1D-PnC comprises branched-open resonators sensor, and a defect guide sandwiched between two PnCs. The structure will be filled with gas samples containing different concentrations of CO₂. The plane wave theory can be used for stationary samples inside the sensor, and the effects of temperature gradients, higher-order modes, and viscosity effects are neglected²³.

Figure 1

Schematic of the 1D-PnC composed of branched open resonators.

The theoretical method used to study the response of the proposed periodic branched open resonators to the incident acoustic waves is called the transfer matrix method (TMM) as the following^{23,24,25,26,27,28,29,30}:

$$M_{i} = \left[ {\begin{array}{*{20}c} {A_{i} } & {B_{i} } \\ {C_{i} } & {D_{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 1 & 0 \\ {y_{R} } & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {A_{i} } & {B_{i} } \\ {C_{i} } & {D_{i} } \\ \end{array} } \right],$$

(1)

where $A_{i} = \cos \left( {k\frac{{d_{i} }}{2}} \right), B_{i} = j Z_{i} sin\left( {k\frac{{d_{i} }}{2}} \right), C_{i} = \frac{j}{{Z_{i} }}sin\left( {k\frac{{d_{i} }}{2}} \right), D_{i}$ = $A_{i}$, $k = {\raise0.7ex\hbox{$\omega $} \!\mathord{\left/ {\vphantom {\omega c}}\right.\kern-0pt} \!\lower0.7ex\hbox{$c$}}$ is the wave number, $\rho$ is the density, $Z_{i} = {\raise0.7ex\hbox{${\rho c}$} \!\mathord{\left/ {\vphantom {{\rho c} {{\text{S}}_{{\text{i}}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{S}}_{{\text{i}}} }$}}$ is the impedance of each period of the proposed branched open resonators, and $c$ is the acoustic speed. The acoustic pressure at the end of the opened lateral chimney is approximately zero, and the acoustic admittance of the acoustic wave ($y_{R} )$ is calculated as:

$$y_{R} = - j \frac{1}{{Z_{2} }} cot\left( {kd_{2} } \right).$$

(2)

For the defect cell:

$$M_{i} = \left[ {\begin{array}{*{20}c} {A_{d} } & {B_{d} } \\ {C_{d} } & {D_{d} } \\ \end{array} } \right],$$

(3)

where $A_{d} = \cos \left( {k\frac{{d_{d} }}{2}} \right), B_{d} = j Z_{d} sin\left( {k\frac{{d_{d} }}{2}} \right), C_{d} = \frac{j}{{Z_{d} }}sin\left( {k\frac{{d_{d} }}{2}} \right), D_{d}$ = $A_{d}$, and $Z_{d} = {\raise0.7ex\hbox{${\rho c}$} \!\mathord{\left/ {\vphantom {{\rho c} {{\text{S}}_{{\text{d}}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{S}}_{{\text{d}}} }$}}$.

Bloch’s theorem is used to plot the dispersion relation of the elementary cell of the 1D-PnC composed of branched open resonators²³:

$${\text{cos}}\left( {Kd} \right) = \cos \left( {kd_{1} } \right) + \frac{M}{2}\sin \left( {kd_{1} } \right)\cot \left( {kd_{2} } \right),$$

(4)

where $K$ is the Bloch vector,$d = d_{1} + d_{2}$, $M = \frac{{S_{2} }}{{S_{1} }}$, k is the wave vector. The transmission and transmittance of the 1D-PnC composed of branched open resonators are calculated as the following:

$$t = \frac{{2\emptyset_{1} }}{{\left( {A_{11} + A_{12} \emptyset_{1} } \right)\emptyset_{1} + \left( {A_{21} + A_{22} \emptyset_{1} } \right)}} ,\;{\text{where}}\;\emptyset_{1} = \frac{1}{z}$$

(5)

$$T\left( \% \right) = 100*\left| t \right|^{2}$$

(6)

Results and discussions

As an initial condition, the geometrical parameters of the main guide and open resonators of the proposed sensors will be N = 10, d₁ = 0.6 m, d₂ = 0.15 m, d_d = 0.3 m, S₁ = 1 m², S₂ = 0.75 m², and S_d = S₁ m². Table 1 shows the acoustic properties of an air sample at different concentrations of CO₂. The gradient of the density of the sample from low to high and acoustic speed from high to low with the increase of the CO₂ concentration ensures that both density and acoustic speed can be considered an indicator of the concentration of CO₂.

Table 1 Acoustic properties of an air sample at different concentrations of CO₂³¹.

The transmittance (red spectra) and dispersion relation (blue spectra) curves versus frequency of the proposed 1D-PnC composed of branched open resonators without defect are plotted and coincided using TMM and Bloch’s theorem in Fig. 2A. In the frequency range of concern, two PhBGs extend from 1429.2 to 1478.1 Hz and from 1950.6 to 2000.6 Hz. The proposed 1D-PnC sensor composed of branched open resonators has the ability to make the PnBG due to the periodic change in the impedance and admittance of propagated acoustic waves inside the structure. By adding a horizontal defect tube sandwiched between two identical 1D-PnCs, a specific frequency of the incident acoustic wave is localized, making a defect peak inside the PnBG. This peak is very sensitive to any change in the mechanical properties of the medium inside the tubes. Considering an additional defect tube with d_d = 0.3 m at the middle of the design and the other geometrical parameters having the same initial values, a resonant peak appears at the center of each PnBG, as clear in Fig. 2B.

Figure 2

(A) The dispersion relation (blue line), the transmittance of the 1D-PnC composed of branched open resonators without defect cell (red line) using air sample (exceed in CO₂ = 0%), and (B) the transmittance with a defect (blue spectrum) using air sample with different CO₂ concentrations.

Any change in the density or acoustic speed of the gas sample due to the change in the CO₂ concentration will result in a transmittance spectrum and cause a wavelength shift to the resonant peaks and PnBGs, as clear in Fig. 3. The defect peak is redshifted to lower frequencies by increasing the concentration of CO₂ from 1975.95 Hz (at 0% of CO₂) to 1872.83 Hz (at 20% of CO₂), 1772.02 Hz (at 40% of CO₂), 1672.36 Hz (at 60% of CO₂), 1612.45 Hz (at 80% of CO₂), and 1575.00 Hz (at 100% of CO₂).

Figure 3

The transmittance of the 1D-PnC sensor composed of branched open resonators with a defect cell using different concentrations of CO₂.

The sensitivity, figure of merit (FoM), quality factor (Q), and detection limit (LoD) of the harmful gas’s sensor are used to examine the efficacy of the sensor and can be defined as follows,

$$S = \frac{{\Delta f_{R} }}{\Delta c},$$

(7)

$$FoM = \frac{S}{FWHM},$$

(8)

$$\begin{array}{*{20}l} {Q = \frac{{f_{R} }}{FWHM}} \hfill \\ \end{array} ,$$

(9)

$$LoD = \frac{{f_{R} }}{20 S Q},$$

(10)

where $\Delta f_{R}$ is the value of the resonant frequency shift with changing the acoustic speed by ($\Delta c$), and FWHM is the peak bandwidth. Sensitivity is the change in the position of the defect peak relative to the acoustic speed relative to the pure air sample as a reference. Q denotes the resonator's energy loss and is expressed as the ratio of the frequency of the defect peak to the FWHM. The sensor's ability to discover the alteration in the resonance frequency is represented by FoM³². LoD denotes the slightest change in the sample that can be detected.

Figure 4A–C shows the S, FWHM, T, FoM, Q, and LoD versus the thickness of d_d. Figure 4A clears the sensitivity and FWHM versus the incident frequency for the proposed 1D-PnC sensor composed of branched open resonators with a defect cell at different d_d values to select the best value that gives the highest performance. The sensitivity is measured for the proposed sensor at different thicknesses of d_d of 0.1 m, 0.2 m, 0.3 m, 0.4 m, 0.5 m, and 0.6 m. In Fig. 4A, the sensitivity is slightly reduced from 5.82 Hz m⁻¹ s to 5.79 Hz m⁻¹ s, 5.76 Hz m⁻¹ s, 5.73 Hz m⁻¹ s, 5.71 Hz m⁻¹ s, and 5.69 Hz m⁻¹ s with the increase of d_d.

Figure 4

(A) S and FWHM, (B) transmittance and FoM, and (C) Q and LoD versus the thickness of d_d.

Sharp defect peaks with 100% intensity at resonant frequencies of 1996.94 Hz, 1986.81 Hz, 1975.95 Hz, 1966.27 Hz, 1958.48 Hz, and 1952.73 Hz for air sample and frequencies of 1591.73 Hz, 1583.67 Hz, 1575.00 Hz, 1567.29 Hz, 1561.08 Hz, and 1556.49 Hz for CO₂ sample at thicknesses of 0.1 m, 0.2 m, 0.3 m, 0.4 m, 0.5 m, and 0.6 m, respectively. The right axis of Fig. 4A clears the variations in the FWHM of the resonant peak with d_d. At d_d = 0.3 m, the FWHM has the lowest value of 0.14 Hz. As a result of the behavior of FWHM, the FoM, and Q have the highest values at the same thickness, according to Eqs. (8) and (9). On the other hand, the LoD has a minor performance at d_d = 0.3 m. d_d = 0.3 m will be the optimum value. This thickness achieved high performance because the resonant peak is located at the center of the PnBG.

The reliability of the 1D-PnC sensor composed of branched open resonators is investigated by studying the impact of the cross-section of S_d on S, FWHM, T, FoM, Q, and LoD at different concentrations of CO₂, as shown in Fig. 5A–C. The defect peak and PnBG exhibit a redshift to lower frequencies as the cross-section of S_d gradually increases. The S decreases from 5.77 to 5.74 Hz m⁻¹ s as the cross-section of S_d increases from 0.9 to 1.4 m². However, the FWHM gradually increases with the cross-section of S_d. Besides, the T of the resonant peak records the highest intensity of (100%). Hence, the FoM and Q gradually decrease, and LoD gradually increases. Depending on the results in Fig. 5A–C, the cross-section of S_d = 1 m² will be used in the following studies.

Figure 5

(A) S and FWHM, (B) transmittance and FoM, and (C) Q and LoD versus the cross-section of S_d.

As d₁ increases from 0.59 m to 0.60 m, 0.61 m, and 0.63 m, the peak of the air sample is redshifted from 2001.36 Hz to 1975.95 Hz, 1950.14 Hz, and 1897.80 Hz, and the peak of the CO₂ sample is redshifted from 1595.26 Hz to 1575.00 Hz, 1554.42 Hz, and 1512.70 Hz. In Fig. 6A, the sensitivity decreases linearly with increasing d₁. On the other hand, FWHM gradually increases with increasing d₁. The transmittance records intensity above 99.9% for thickness d₁ higher than 0.59 m, as clear in Fig. 6B,C. Besides, FoM and Q gradually decrease, and LoD gradually increases with increasing d₁. Therefore, a thickness of 0.59 m will be optimum.

Figure 6

(A) S and FWHM, (B) transmittance and FoM, and (C) Q and LoD versus the thickness of d₁.

Figure 7A clears the sensitivity and FWHM versus the incident frequency for the proposed 1D-PnC sensor composed of branched open resonators with a defect cell at different values of d₂ to select the best value that gives the highest performance. The sensitivity is measured for the proposed sensor at different thicknesses of d₂ of 0.148 m, 0.149 m, 0.15 m, and 0.152 m. In Fig. 7A, the sensitivity is increased from 4.30 Hz m⁻¹ s to 5.84 Hz m⁻¹ s with the increase of d₂ from 0.148 m to 0.149 m. Then, sensitivity slightly decreases to 5.83 Hz m⁻¹ s with the increase of d₂ to 0.150 m. After that, sensitivity is significantly reduced to 4.29 Hz m⁻¹ s with the increase of d₂ to 0.152 m. At d₂ = 0.150 m, the FWHM has the lowest value of 0.068 Hz. The T of the resonant peak changes from 99.24% to 93.26%, 94.15%, and 99.76% by changing the thickness of d₂ from 0.148 m to 0.149 m, 0.15 m, and 0.152 m. As a result of the behavior of FWHM and sensitivity, the FoM and Q have the highest values at the same thickness, according to Eqs. (8) and (9) and Fig. 7B,C. On the other hand, the LoD has the smallest performance at d₂ = 0.150 m. d₂ = 0.150 m will be the optimum value.

Figure 7

(A) S and FWHM, (B) transmittance and FoM, and (C) Q and LoD versus the thickness of d₂.

Figure 8A–C shows the variations in S, FWHM, T, FoM, Q, and LoD with cross-sections S₂. The defect peak and PnBG exhibit a redshift to lower frequencies as the cross-section of S₂ gradually increases. The S gradually decreases from 5.84 to 5.83 Hz m⁻¹ s as the cross-section of S_d increases from 0.71 to 0.85 m². Also, the FWHM gradually decreases with the increase of the cross-section of S₂ for all selected values of cross-sections except at 0.79 m² and 85 m². At these values (0.79 m² and 85 m²), the FWHM records a small increase. The T of the resonant peak changes from 94.97% to 97.18%, 94.15%, 95.07%, 77.00%, 94.46%, 90.5%, and 66.48% by changing the cross-section of S₂ from 0.71 m² to 0.73 m², 0.75 m², 0.77 m², 0.79 m², 0.81 m², 0.83 m², and 0.85 m². FoM changes from 64.68 m⁻¹ s to 75.45 m⁻¹ s, 85.42 m⁻¹ s, 97.58 m⁻¹ s, 89.94 m⁻¹ s, 130.54 m⁻¹ s, 140.90 m⁻¹ s, and 109.83 m⁻¹ s by changing the cross-section of S₂ from 0.71 m² to 0.73 m², 0.75 m², 0.77 m², 0.79 m², 0.81 m², 0.83 m² and 0.85 m². Besides, Q changes from 22,183.31 to 25,879.92, 29,298.19, 33,472.38, 30,849.29, 44,775.59, 48,326.07, and 37,670.87 by changing the cross-section of S₂ from 0.71 m² to 0.73 m², 0.75 m², 0.77 m², 0.79 m², 0.81 m², 0.83 m², and 0.85 m². On the other hand, LoD changes from 8 × 10^–4 m s⁻¹ to 7 × 10^–4 6 × 10^–4 m s⁻¹, 5 × 10^–4 m s⁻¹, 6 × 10^–4 m s⁻¹, 4 × 10^–4 m s⁻¹, 4 × 10^–4 m s⁻¹ and 5 × 10^–4 m s⁻¹ by changing the cross-section of S₂ from 0.71 m² to 0.73 m², 0.75 m², 0.77 m², 0.79 m², 0.81 m², 0.83 m² and 0.85 m². As a result, 0.83 m² will be the optimum cross-section.

Figure 8

(A) S and FWHM, (B) transmittance and FoM, and (C) Q and LoD versus the cross-section of S₂.

At selected conditions, the defect peak is redshifted to lower frequencies by increasing the concentration of CO₂ from 1999.02 Hz (at 0% of CO₂) to 1894.7 Hz (at 20% of CO₂), 1792.71 Hz (at 40% of CO₂), 1691.89 Hz (at 60% of CO₂), 1631.27 Hz (at 80% of CO₂), and 1593.39 Hz (at 100% of CO₂), as clear in Fig. 9A. This redshift of the PnBG and resonant peak to lower frequencies is due to the direct proportionality between the acoustic speed of the sample and the resonant frequency according to the standing wave equation:

$$2d = \frac{nc}{f},$$

(11)

where d and n are the thickness and an integer, respectively. In Fig. 9B, the acoustic speed and resonant frequency versus the concentration of CO₂ are plotted. An empirical equation between the resonant frequency ($f_{R}$) and the concentration of CO₂ ($C_{CO2}$) was established using the quadric fitting as the following relation:

$$f_{R} = 0.02222{ }C_{CO2}^{2} - 6.392{ }C_{CO2} + { }2005,{ }\left( {R^{2} = 0.9975} \right).$$

(12)

Figure 9

(A) The transmittance at selected conditions using air samples with different CO₂ concentrations, and (B) acoustic speed and resonant frequency versus the concentration of CO₂.

By fitting the simulated data, by knowing the resonant frequency, the CO₂ concentration can be predicted according to the following equation:

$$C_{CO2} = - 1.7656 \times 10^{ - 6} { }f_{R}^{3} + { }0.009803{ }f_{R}^{2} - { }18.299f_{R} + 11511$$

(13)

Conclusion

This study proposed a branched open resonator sensor with a defect guide sandwiched between two PnCs. The structural properties and geometrical parameters of the 1D-PnC sensor composed of branched open resonators were thoroughly optimized. The above simulation studies indicate that the suggested 1D-PnC composed of branched open resonators can effectively detect the concentration of CO₂ with a sensitivity of 5.8 Hz m⁻¹ s, FoM of 140 m⁻¹.s, Q of 5 × 10⁴, and LoD of 4 × 10^–4. Using branched open resonators enhanced the sensor’s performance, according to Table 2. As a result, the suggested design could be useful in different sensing and filtering devices.

Table 2 Comparison study.