1 Introduction

Laser interference technology [1,2,3] was developed after the establishment of the laser knowledge system. With characteristics of good monochromaticity, strong directivity and high brightness, laser quickly enters various industries. The organic combination of laser and laser interference technology promoted the development of technology. Now, it has been widely used in various fields such as industry, agriculture, medicine, military and scientific research [4, 5], which has promoted the advancement of technology. In an ideal homogeneous medium, the obtained laser interference image is perfect, but the existence of atmospheric turbulence has a significant influence on the results of laser interference [6,7,8,9]. Atmospheric turbulence is a random variation of atmospheric refractive index and temperature due to solar radiation and various meteorological factors [10,11,12,13], and these changes fluctuate within the magnitude range of 10–6 [14]. Because of this fluctuation, the laser fluctuates in phase randomly during transmission, which is manifested by beam quivering, intensity flicking, and cross section expansion. This inevitably changes the measurement results of the interference, thereby affecting the restoration and analysis of the detection target.

Beginning with the transmission equation of laser in turbulent medium, this paper studies the statistical model of laser intensity and contrast in the atmospheric transmission and then studies the degree of influence of laser source characteristics and transmission distance on the contrast, to further describe the properties of laser interference. This issue has practical significance for the research of laser interference technology and provides a theoretical basis for the detection of laser interference targets.

2 Method

The equation for the laser transmission in turbulent medium [15, 16] is

$$ 2ik\frac{\partial A}{{\partial z}} + \frac{{\partial^{2} A}}{{\partial x^{2} }} + \frac{{\partial^{2} A}}{{\partial y^{2} }} + k^{2} A\tilde{\varepsilon }\left( {\varvec{\varrho },{\varvec{z}}} \right) = 0 $$
(1)

where A is the amplitude, \(\widetilde{\varepsilon }\left(\varvec{\varrho },{\varvec{z}}\right)\) is the fluctuating dielectric constant affected by the laser cross-section coordinates and transmission distance, \(x\) and \(y\) are the orthogonal coordinates of the laser cross section, respectively, and z is the transmission distance. According to the substitution of equal quantity

$$ 2ik\frac{\partial A}{{\partial z}} + k^{2} A\tilde{\varepsilon }\left( {\varvec{\varrho },{\varvec{z}}} \right) = 2ikexp\left[ { - \frac{{k^{2} }}{2ik}\mathop \int \limits_{0}^{z} \tilde{\varepsilon }\left( {\varvec{\varrho },\xi } \right)d\xi } \right]\frac{\partial }{\partial z}\left\{ {Aexp\left[ {\frac{{k^{2} }}{2ik}\mathop \int \limits_{0}^{z} \tilde{\varepsilon }\left( {\varvec{\varrho },\xi } \right)d\xi } \right]} \right\} $$
(2)

After Eq. (2) is substituted into Eq. (1), we obtain

$$ 2ik\frac{\partial }{\partial z}\left\{ {Aexp\left[ { - \frac{ik}{2}\mathop \int \limits_{0}^{z} \tilde{\varepsilon }\left( {\varvec{\varrho },\xi } \right)d\xi } \right]} \right\} = - exp\left[ { - \frac{ik}{2}\mathop \int \limits_{0}^{z} \tilde{\varepsilon }\left( {\varvec{\varrho },\xi } \right)d\xi } \right]\left( {\frac{{\partial^{2} A}}{{\partial x^{2} }} + \frac{{\partial^{2} A}}{{\partial y^{2} }}} \right) $$
(3)

where \(A = A\left( {\varvec{\varrho },{\varvec{z}}} \right)\). After performing integral collation on the above equation, we obtain

$$ 2ikA\left( {\varvec{\varrho },{\varvec{z}}} \right) - 2ikA_{0} exp\left[ {\frac{ik}{2}\mathop \int \limits_{0}^{z} \tilde{\varepsilon }\left( {\varvec{\varrho },\xi } \right)d\xi } \right] = - \mathop \int \limits_{0}^{z} dz^{\prime}exp\left[ {\frac{ik}{2}\mathop \int \limits_{z^{\prime}}^{z} \tilde{\varepsilon }\left( {\varvec{\varrho },\xi } \right)d\xi } \right]\left( {\frac{{\partial^{2} A\left( {\varvec{\varrho },z^{\prime}} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} A\left( {\varvec{\varrho },z^{\prime}} \right)}}{{\partial y^{2} }}} \right) $$
(4)

Suppose \({\varvec{\varrho }}_{1}\) is the transverse coordinate of the adjacent integral cross section in the turbulent medium, then it satisfies

$$ 2ik\frac{{\partial A\left( {\varvec{\varrho }_{1} ,{\varvec{z}}} \right)}}{\partial z} + \frac{{\partial^{2} A\left( {\varvec{\varrho }_{1} ,{\varvec{z}}} \right)}}{{\partial x^{2} }} + \frac{{\partial^{2} A\left( {\varvec{\varrho }_{1} ,{\varvec{z}}} \right)}}{{\partial y^{2} }} + k^{2} A\left( {\varvec{\varrho }_{1} ,{\varvec{z}}} \right)\tilde{\varepsilon }\left( {\varvec{\varrho }_{1} ,{\varvec{z}}} \right) = 0 $$
(5)

Let the mutual function of m, n moments [17] are

$$ \Gamma_{m,n} = A\left( {\varvec{\varrho }_{1} ,{\varvec{z}}} \right)A\left( {\varvec{\varrho }_{2} ,{\varvec{z}}} \right) \cdot \cdot \cdot A\left( {\varvec{\varrho }_{{\varvec{m}}} ,{\varvec{z}}} \right)A^{*} \left( {\varvec{\varrho }_{1}^{{^{\prime}}} ,{\varvec{z}}} \right)A^{*} \left( {\varvec{\varrho }_{2}^{{^{\prime}}} ,{\varvec{z}}} \right) \cdot \cdot \cdot A^{*} \left( {\varvec{\varrho }_{{\varvec{n}}}^{{^{\prime}}} ,{\varvec{z}}} \right) = \gamma $$
(6)

Then substitute the complex conjugate Eq. \(2ik\frac{{\partial A^{*} }}{\partial z} - \frac{{\partial^{2} A^{*} }}{{\partial x^{2} }} - \frac{{\partial^{2} A^{*} }}{{\partial y^{2} }} - k^{2} A^{*} \tilde{\varepsilon } = 0\) of Eq. (1) into Eq. (5)

$$ 2ikA\left( {\varvec{\varrho }_{1} ,{\varvec{z}}} \right) \cdot \cdot \cdot A\left( {\varvec{\varrho }_{{\varvec{m}}} ,{\varvec{z}}} \right)\frac{{\partial A^{*} \left( {\varvec{\varrho }_{1}^{{^{\prime}}} ,{\varvec{z}}} \right)}}{\partial z}A^{*} \left( {\varvec{\varrho }_{2}^{{^{\prime}}} ,{\varvec{z}}} \right) \cdot \cdot \cdot A^{*} \left( {\varvec{\varrho }_{{\varvec{n}}}^{{^{\prime}}} ,{\varvec{z}}} \right) - \nabla_{1}^{2} \gamma - k^{2} \gamma \tilde{\varepsilon }\left( {\varvec{\varrho }_{1}^{{^{\prime}}} ,{\varvec{z}}} \right) = 0 $$
(7)

Let

$$ \hat{L} = \nabla_{1}^{2} + \ldots + \nabla_{m}^{2} - \nabla_{1}^{2^{\prime}} - \ldots - \nabla_{n}^{2^{\prime}} $$
(8)
$$ \hat{\varepsilon } = \tilde{\varepsilon }\left( {\varvec{\varrho }_{1} ,{\varvec{z}}} \right) + \ldots + \tilde{\varepsilon }\left( {\varvec{\varrho }_{{\varvec{n}}} ,{\varvec{z}}} \right) - \tilde{\varepsilon }\left( {\varvec{\varrho }_{1}^{{^{\prime}}} ,{\varvec{z}}} \right) - \ldots - \tilde{\varepsilon }\left( {\varvec{\varrho }_{{\varvec{n}}}^{{^{\prime}}} ,{\varvec{z}}} \right) $$
(9)

Then, Eq. (1) can be written as:

$$ 2ik\frac{\partial \gamma }{{\partial z}} + \gamma \hat{L} + \gamma k^{2} \hat{\varepsilon } = 0 $$
(10)

Combined with Eq. (6), the above equation can be written as

$$ \frac{{\partial \Gamma_{m,n} }}{\partial z} - \frac{i}{2k}\hat{L}\Gamma_{m,n} + \frac{{k^{2} \Gamma_{m,n} }}{8} = 0 $$
(11)

For convenience of expression, the parameter \(\overline{\varvec{\varrho } }=\frac{\varvec{\varrho }+\varvec{\varrho }\boldsymbol{^{\prime}}}{2}\), \({\varvec{\varrho }}^{\mathbf{*}}=\varvec{\varrho }-\varvec{\varrho }\boldsymbol{^{\prime}}\) is imported, then Eq. (11) is written as

$$ \frac{{\partial \Gamma \left( {\varvec{\varrho}}^{*},\overline{\varvec{\varrho}},{\varvec{z}} \right)}}{\partial z} -\frac{i}{k}\frac{{\partial^{2} \Gamma }}{{\partial {\varvec{\varrho}}^{{*}} \partial\overline{\varvec{\varrho}}}} +\frac{{pik^{2}\Gamma }}{4}H\left( {\varvec{\varrho}}^{{*}} \right)= 0 $$
(12)

where \(H({\varvec{\varrho }}^{\boldsymbol{*}})\) is the transverse coherence coefficient of the amplitude. Through the Fourier transform relationship of \(\overline{\varvec{\varrho } }\), we obtain

$$ \Gamma \left( {\varvec{\varrho }^{{*}} ,{\varvec{\overline{\varrho}}},{\varvec{z}}} \right) = \int \gamma \left( \varvec{\varrho^{*} ,{\varvec{p}},z} \right)exp\left( {i{\varvec{p}} \cdot {\varvec{\overline{\varrho}}}} \right)d^{2} p $$
(13)

where \(p=\frac{k(\varrho -\varvec{\varrho }^{*})}{z}\) is a parameter imported for convenience of calculation. Combine the above two equations, we obtain

$$ \frac{\partial \gamma }{{\partial z}} + \frac{{\varvec{p}}}{k}\frac{\partial \gamma }{{\partial \varvec{\varrho }^{{*}} }} + \frac{{\pi k^{2} \gamma }}{4}H\left( {\varvec{\varrho }^{{*}} } \right) = 0 $$
(14)

Based on Taylor Expansion

$$ f\left( {\varvec{\varrho }^{{*}} + \varvec{\varrho }_{0} } \right) = exp\left( {\varvec{\varrho }_{0} \frac{\partial }{{\partial \varvec{\varrho }^{{*}} }}} \right)f\left( {\varvec{\varrho }^{{*}} } \right) $$
(15)

Equation (14) can be written as

$$ \frac{\partial }{\partial z}\left[ {exp\left( {\frac{{{\varvec{pz}}}}{k}\frac{\partial }{{\partial \varrho^{*} }}} \right)\gamma \left( {\varvec{\varrho }^{{*}} ,{\varvec{p}},{\varvec{z}}} \right)} \right] = - \frac{{\pi k^{2} }}{4}exp\left( {\frac{{{\varvec{pz}}}}{k}\frac{\partial }{{\partial \varvec{\varrho }^{{*}} }}} \right)\left[ {H\left( {\varvec{\varrho }^{{*}} } \right)\gamma \left( {\varvec{\varrho }^{{*}} ,{\varvec{p}},{\varvec{z}}} \right)} \right] $$
(16)

In combination with Eq. (13), we have

$$ \Gamma \left( {\varvec{\varrho }^{{*}} ,{\varvec{\overline{\varrho}}},{\varvec{z}}} \right) = \int \gamma_{0} \left( {\varvec{\varrho }^{{*}} - \frac{{{\varvec{pz}}}}{k},{\varvec{p}}} \right)exp\left\{ {i{\varvec{p}} \cdot {\varvec{\overline{\varrho}}} - \frac{{\pi k^{2} }}{4}\mathop \int \limits_{0}^{z} H\left[ {\varvec{\varrho }^{{*}} - \frac{{\varvec{p}}}{k}\left( {{\varvec{z}} - \xi } \right)} \right]d\xi } \right\}d^{2} p $$
(17)

In the above equation

$$ \gamma_{0} \left( {\varvec{\varrho }^{{*}} ,{\varvec{p}}} \right) = \frac{1}{{4\pi^{2} }}\int \exp \left( { - i{\varvec{p}} \cdot {\varvec{\overline{\varrho}}}^{{^{\prime}}} } \right){\Gamma }^{\left( 0 \right)} \left( {\varvec{\varrho }^{{*}} ,{\varvec{\overline{\varrho}}}^{{^{\prime}}} } \right)d^{2} {\varvec{\overline{\varrho}}}^{{^{\prime}}} $$
(18)

where \({\overline{\varvec{\varrho }} }^{\boldsymbol{^{\prime}}}\) is a functional parameter [18]. Substituting \(p=\frac{k(\varrho -\varvec{\varrho }^{*})}{z}\) into Eq. (17), we obtain

$$ \Gamma \left( {\varvec{\varrho }^{{*}} ,{\varvec{\overline{\varrho}}},{\varvec{z}}} \right) = \frac{{k^{2} }}{{4\pi^{2} {\varvec{z}}^{2} }}\int d^{2} \varvec{\varrho }d^{2} {\varvec{\overline{\varrho}}}^{{^{\prime}}} {\Gamma }^{\left( 0 \right)} \left( {\varvec{\varrho },{\varvec{\overline{\varrho}}}^{{^{\prime}}} } \right)exp\left\{ {\frac{ik}{{\varvec{z}}}\left( {\varvec{\varrho }^{{*}} - \varvec{\varrho }} \right)\left( {{\varvec{\overline{\varrho}}} - {\varvec{\overline{\varrho}}}^{{^{\prime}}} } \right) - \frac{{\pi k^{2} }}{4}\mathop \int \limits_{0}^{z} H\left[ {\frac{{\varvec{\varrho }^{{*}} \xi }}{{\varvec{z}}} + \varrho \left( {1 - \frac{\xi }{{\varvec{z}}}} \right)} \right]d\xi } \right\} $$
(19)

The average laser intensity is obtained by \({\varvec{\varrho }}^{\boldsymbol{*}}=0\)

$$ I\left( {{\varvec{\overline{\varrho}}},{\varvec{z}}} \right) = \frac{{k^{2} }}{{4\pi^{2} {\varvec{z}}^{2} }}\int d^{2} \varvec{\varrho }\int d^{2} {\varvec{\overline{\varrho}}}^{{^{\prime}}} {\Gamma }^{\left( 0 \right)} \left( {\varvec{\varrho },{\varvec{\overline{\varrho}}}^{{^{\prime}}} } \right)exp\left\{ { - \frac{{ik\varvec{\varrho }}}{{\varvec{z}}}\left( {{\varvec{\overline{\varrho}}} - {\varvec{\overline{\varrho}}}^{{^{\prime}}} } \right) - \frac{{\pi k^{2} }}{4}\mathop \int \limits_{0}^{z} H\left[ {\varvec{\varrho }\left( {1 - \frac{\xi }{{\varvec{z}}}} \right)} \right]d\xi } \right\} $$
(20)

If the cross section radius at the laser source is \( a\), the above formula can be further written as

$$ I\left( {{\varvec{\overline{\varrho}}},{\varvec{z}}} \right) = \frac{{k^{2} a^{2} A_{0}^{2} }}{{4\pi {\varvec{z}}^{2} }}\int d^{2} \varvec{\varrho } \cdot exp\left[ { - \frac{{ik{\varvec{\overline{\varrho}}}^{{^{\prime}}} \cdot \varvec{\varrho }}}{{\varvec{z}}} - \frac{{\varvec{\varrho }^{2} \left( {1 + \frac{{k^{2} a^{4} }}{{{\varvec{z}}^{2} }}} \right)}}{{4a^{2} }} - \frac{{\pi k^{2} {\varvec{z}}}}{4}\mathop \int \limits_{0}^{1} H\left( {\varvec{\varrho }\tau } \right)d\tau } \right] $$
(21)

where \(A_{0}\) is the initial amplitude of the emitted laser. Write the above equation in the polar coordinates form, we have

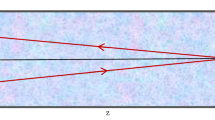
$$ I\left( {{\varvec{\overline{\varrho}}},{\varvec{z}}} \right) = \frac{{k^{2} a^{2} A_{0}^{2} }}{{4\pi z^{2} }}\mathop \int \limits_{0}^{\infty } \varvec{\varrho }d\varvec{\varrho } \cdot exp\left[ { - \frac{{\varvec{\varrho }^{2} ({\varvec{z}}^{2} + k^{2} a^{4} )}}{{4a^{2} {\varvec{z}}^{2} }} - \frac{{3\pi \varvec{\varrho }^{{*}} }}{32}C_{\varepsilon }^{2} k^{2} {\varvec{z}}\varvec{\varrho }^{\frac{5}{3}} } \right] \cdot \mathop \int \limits_{0}^{2\pi} exp\left( {\frac{{ik\varvec{\varrho \varvec{\overline{\varrho}}}}}{{\varvec{z}}}cos\phi } \right)d\phi $$
(22)

Assume that the reflecting plane is an ideal reflector and does not change the laser transmission characteristics. Interfering it with the reference light, we obtain a target interference image of the turbulent atmosphere, as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of laser detection interference in turbulent atmosphere

Full size image

where the \({I}_{1}\) optical path is the reference light, the direction of which can be considered as along the axis, and the laser intensity of which is expressed as

$$ I_{0} \left( z \right) = \frac{{k^{2} a^{2} A_{0}^{2} }}{{2{\varvec{z}}^{2} }}\mathop \int \limits_{0}^{\infty } exp\left( { - \frac{{\varvec{\varrho }^{*2} \left( {{\varvec{z}}^{2} + k^{2} a^{4} } \right)}}{{4a^{2} {\varvec{z}}^{2} }}} \right)\varvec{\varrho }^{{*}} d\varvec{\varrho }^{{*}} = \frac{{k^{2} a^{4} A_{0}^{2} }}{{z^{2} + k^{2} a^{4} }} $$
(23)

According to the relationship between interference contrast and laser intensity

$$ K = \frac{{\overline{I} - I_{0} }}{{\overline{I} + I_{0} }} $$
(24)

The laser interference contrast of the turbulent atmospheric medium is obtained.

3 Results and discussion

With the laser light source as the coordinate origin and the laser transmission distance taken as500m, the characteristic curve showing the laser intensity changing with the laser cross section radius can be obtained, as shown in Fig. 2.

Fig. 2
figure 2

Relationship between laser cross section radius and light intensity at z = 500 m

Full size image

According to the above figure, the intensity of the transmitted laser increases as the laser cross section radius increases, indicating that in the actual detection, the visibility of the interference image can be improved by increasing the cross section radius appropriately. When the cross section radius was taken as 1 mm, we observed the influence of the transmission distance on the intensity in the turbulent medium, as shown in Fig. 3.

Fig. 3
figure 3

Relationship between laser transmission distance and intensity at a = 1 mm

Full size image

From the above figure, it can be clearly observed that the laser intensity decreases significantly with the increase of the laser transmission distance in the atmospheric turbulent medium. In the case of a = 1 mm, the transmission distance being less than 1000 m can cause the almost complete attenuation of the intensity. Therefore, it is necessary to appropriately increase the cross section radius or to implement gain on the intensity in practical applications so that the beam is transmitted farther.

When we put the reference light in Fig. 1 into the air without turbulence and assume that the surface of the detection target is an ideal reflection surface, it is considered that no change in properties such as phase and intensity occurs in the reflection process. If the laser transmission distance is 300 m, 600 m and 800 m, respectively, the relationship between the laser cross section radius and the interference contrast is observed, as shown in Fig. 4.

Fig. 4
figure 4

Comparison of relationship between laser cross section radius and interference contrast at different transmission distances

Full size image

From the above figure, it can be seen that the contrast cannot be detected when the laser cross section radius is just greater than zero due to the influence of the atmospheric turbulent medium. With the increase of the cross section radius, the contrast increases sharply and tends to be stable over a certain range. As the cross section radius continues to increase, the interference contrast will present a decrease trend. Figure 4 also shows that the larger the transmission distance, the lower the overall interference contrast, and the final decrease tends to be relatively significant.

If the laser cross section radius is taken as fixed values of 2 mm, 3 mm, and 4 mm, respectively, the relationship between the laser transmission distance and the interference contrast may be observed, as shown in Fig. 5.

Fig. 5
figure 5

Comparison of relationship between laser transmission distance and interference contrast at different cross section radii

Full size image

As seen from the above figure, the laser transmission distance and the interference contrast are basically the same at different cross section radius values. As the transmission distance increases from 0, the interference contrast slowly decreases, and then, a large drop occurs and lasts until it almost reaches zero, failing to obtain the interference information. However, as the distance continues to increase, the interference contrast has a small fluctuation.

To study the influence of laser cross section radius and transmission distance on interference contrast more intuitively, the three may be presented in the same picture, as shown in Fig. 6.

Fig. 6
figure 6

Research on interference characteristics of laser transmission based on atmospheric turbulent medium

Full size image

Based on above, in the transmission process with a small laser cross section radius, a small fluctuation occurs after the interference contrast drops to zero, but the contrast will not exceed 0.2. When the laser cross section radius is large, the interference contrast at a close distance is large, and interference fringes can be obtained easily. Therefore, the appropriate cross section radius shall be selected depending on the detection distance in practical applications. Due to the influence of atmospheric turbulence, the interference contrast at a long distance will drop to a zero regardless of the cross section radius. Therefore, to detect a distant target, it is necessary to perform gain on the laser intensity or improve the phase information.

Figure 7 shows the actual detection of laser interference radar [19]. The marked area in Fig. 7b is a strong interference area, and the other bright areas are ordinary interference areas. In addition to the reflection characteristics of the reflecting surface, the near-field target has a relatively clear and accurate interference spectrum, while the interference effect of the distant target is not ideal, and even the interference contrast of some targets almost drops to zero. In such cases, the recognition is impossible (such as high-rise building at the right front). The laser interference effect under atmospheric turbulent medium has obvious influence on the actual measurement. To obtain the detection target more accurately, it is of great significance to develop the laser interferometry technology for atmospheric turbulent medium.

Fig. 7
figure 7

Actual detection map of laser interference radar, a target to be detected, b laser interference image

Full size image

4 Conclusions

This paper studies the interference of various factors on the intensity and contrast of laser transmission in the atmospheric turbulence medium. When the transmission distance is constant, the laser intensity increases with the increase of the cross section radius. When the laser cross section radius is constant, the intensity attenuates sharply with increase of the transmission distance. The laser interference contrast of the atmospheric turbulent medium is also low when the cross section radius is small, the fluctuation amplitude is also small, and there are two peak values at this time. When the cross section radius is large, the interference contrast fluctuates sharply, and the interference contrast of the near field is high and rapidly decreases when reaching the far field until it approaches zero. By contrast, the transmission distance has a significant influence on the laser interference.

To increase the laser interference contrast in the atmospheric turbulence, the detection results can also be improved by means of laser intensity gaining, phase correction, image processing, and the like in addition to appropriately increasing the cross section radius. In future work, we will further analyze the above factors and consider various influencing factors comprehensively to obtain a more reasonable improvement method and provide a strong guarantee for the laser detection technology.