Multiple timescale mixed bursting dynamics in a respiratory neuron model

Abstract

Experimental results in rodent medullary slices containing the pre-Bötzinger complex (pre-BötC) have identified multiple bursting mechanisms based on persistent sodium current (I _NaP) and intracellular Ca²⁺. The classic two-timescale approach to the analysis of pre-BötC bursting treats the inactivation of I _NaP, the calcium concentration, as well as the Ca²⁺-dependent inactivation of IP ₃ as slow variables and considers other evolving quantities as fast variables. Based on its time course, however, it appears that a novel mixed bursting (MB) solution, observed both in recordings and in model pre-BötC neurons, involves at least three timescales. In this work, we consider a single-compartment model of a pre-BötC inspiratory neuron that can exhibit both I _NaP and Ca²⁺ oscillations and has the ability to produce MB solutions. We use methods of dynamical systems theory, such as phase plane analysis, fast-slow decomposition, and bifurcation analysis, to better understand the mechanisms underlying the MB solution pattern. Rather surprisingly, we discover that a third timescale is not actually required to generate mixed bursting solutions. Through our analysis of timescales, we also elucidate how the pre-BötC neuron model can be tuned to improve the robustness of the MB solution.

Appendices

Appendix: A: Adjusting timescales in the dendritic subsystem

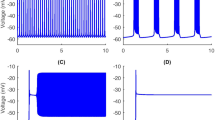
The full model (1a) is capable of generating an MB solution (Fig. 21A) using parameter values for which ([Ca],l) acts as a relaxation oscillator ([IP3]=0.95 μM, A=0.005 μM⁻¹⋅m s ⁻¹ as in (Park and Rubin 2013)). However, since the l-nullcline lies extremely close to the left knee of [Ca]-nullcline (Fig. 21B), the trajectory projected to ([Ca],l)-space does not jump up to large [Ca] values and transition to the long burst (LB) phase immediately after passing the left knee (yellow circle). Instead, it slowly moves along the l-nullcline for a transient period before jumping up to the right branch (Fig. 21B and C: from the yellow circle to the green circle); this effect can be interpreted as the influence of the bifurcation in the dendritic subsystem that initiates the (c,l) oscillation, which occurs at a value of [IP₃] just below 0.95 (Park and Rubin 2013). Numerically, we observe that small bursts occur during this period (Fig. 21A). Therefore, the existence of the MB solution relies heavily on the nullcline interactions, which can be tuned by changing [IP₃]. To clarify the identification of the timescales involved in the MB behavior and the assessment of how to group timescales, and to eliminate the sensitivity of MB solutions to the precise value of [IP₃], we increase [IP₃] to 1. As a result, the [Ca]-nullcline moves downward and hence further from the l-nullcline. Furthermore, we also slow down l by decreasing A from 0.005 to 0.001 so that l∼O(1000) ms becomes more separated from [Ca], the delay time of the jump up of [Ca] at the left knee is significantly decreased, and the dendritic subsystem takes on a stronger relaxation character.

Fig. 21

Time series for attracting solutions of the full model (1a) as well as the bifurcation structure of the dendritic subsystem with parameter values as in Table 1 except [IP3]=0.95[μM], A=0.005[μM⁻¹⋅m s ⁻¹] as in (Park and Rubin 2013). Green and yellow symbols mark key points along the solution trajectory (green star: the point with minimum g _{CAN T o t} ; yellow circle: the point when the trajectory passes the left knee of the [Ca]-nullcline; green circle: beginning of the long burst (LB).) (A): Time series for V. (B): Enlarged view of part of Fig. 2B showing the nullclines for [Ca] (red) and l (cyan) for the dendritic subsystem, together with the MB solution from the upper row. (C): Part of time series of [Ca]

Remark 1

Although the dendritic subsystem acts as a more standard relaxation oscillator with the new parameter values ([IP₃]=1, A=0.001), [IP₃] is not far enough from the bifurcation value for the influence of the bifurcation mentioned above to completely vanish. Hence, there is still a transient delay before [Ca] jumps up at the left knee, but it is much shorter than that with original parameter values.

Appendix: B: Nondimensionalization of the full model (1a)

From numerical simulations, we find that the membrane potential V typically lies between −60 mV and 20 mV. Correspondingly, for x∈{n,h}, we define T _x = max(1/τ _x (V)) over the range V∈[−60,20] and then define t _x (V), a rescaled version of τ _x (V), by t _x (V)=T _x τ _x (V). We also define g _max to be the maximum of the five conductances g _L, g _K, g _Na, g _NaP and g _CAN. Furthermore, we let $G([\text {Ca}])=\frac {[\mathrm {IP_{3}}][\text {Ca}]} {([\mathrm {IP_{3}}]+K_{I})([\text {Ca}]+K_{a})}$ and $g_{\text {SERCA}}([\text {Ca}])=V_{\text {SERCA}}\frac {[\text {Ca}]}{K^{2}_{\text {SERCA}}+[\text {Ca}]^{2}}$. Substituting these expressions into Eq. (1a) and rearranging, we obtain the following system:

$$\begin{array}{@{}rcl@{}} \frac{C_{m}}{Q_{t}\cdot g_{\max}}\frac{dv}{d\tau}&=&-\bar{g}_{\mathrm{L}}(v-\bar{V}_{\mathrm{L}})-\bar{g}_{\mathrm{K}}n^{4}(v-\bar{V}_{\mathrm{K}})\\ &&-\bar{g}_{\text{Na}}m_{\infty}^{3}(v)(1-n)(v-\bar{V}_{\text{Na}})\\ &&-\bar{g}_{\text{NaP}}mp_{\infty}(v)h(v-\bar{V}_{\text{Na}})\\ &&-\bar{g}_{\text{CAN}}f(c)(v-\bar{V}_{\text{Na}}) \end{array} $$

(7a)

$$\begin{array}{@{}rcl@{}} \frac{1}{Q_{t}\cdot T_{n}} \frac{dn}{d\tau}&=&(n_{\infty}(v)-n)/{t_{n}(v)} \end{array} $$

(7b)

$$\begin{array}{@{}rcl@{}} \frac{1}{Q_{t}\cdot T_{h}} \frac{dh}{d\tau}&=&(h_{\infty}(v)-h)/{t_{h}(v)} \end{array} $$

(7c)

$$\begin{array}{@{}rcl@{}} \frac{d[\text{Ca}]}{d\tau}&=& K_{Ca}\cdot(L_{{\text{IP}}_{3}}+P_{{\text{IP}}_{3}}G^{3}([\text{Ca}]) l^{3})\\&&\times(\frac{[\text{Ca}]_{\text{Tot}}-[\text{Ca}]}{\sigma}-[\text{Ca}]) \end{array} $$

(7d)

$$\begin{array}{@{}rcl@{}} &&-K_{Ca}\cdot g_{\text{SERCA}}([\text{Ca}])\cdot [\text{Ca}] \\ \frac{dl}{d\tau}&=& AK_{\mathrm{d}}(1-l)-A[\text{Ca}] l\ \end{array} $$

(7e)

with dimensionless parameters $\bar {g}_{x}=g_{x}/g_{\max }$ and $\bar {V}_{x}=V_{x}/Q_{v}$. Note that we have now nondimensionalized the somatic subsystem (1a)-(1c).

Next we deal with Eqs. (1d)-(1e) by nondimensionalizing [Ca], which typically lies between 0 μM and 1 μM, based on numerical simulations. We define G _c = max(G ³([Ca])) and G _S = max(g _SERCA(Ca)) over the range [Ca]∈[0,1] and then define P _max to be the maximum of { _{L IP 3},P _{IP 3} G _c ,G _S }. From system (7a), we get the following dimensionless system:

$$\begin{array}{@{}rcl@{}} \frac{C_{m}}{Q_{t}\cdot g_{\max}}\frac{dv}{d\tau}&=&-\bar{g}_{\mathrm{L}}(v-\bar{V}_{\mathrm{L}})-\bar{g}_{\mathrm{K}}n^{4}(v-\bar{V}_{\mathrm{K}})\\ &&-\bar{g}_{\text{Na}}m_{\infty}^{3}(v)(1-n)(v-\bar{V}_{\text{Na}})\\ &&-\bar{g}_{\text{NaP}}mp_{\infty}(v)h(v-\bar{V}_{\text{Na}})\\ &&-\bar{g}_{\text{CAN}}f(c)(v-\bar{V}_{\text{Na}}) \end{array} $$

(8a)

$$\begin{array}{@{}rcl@{}} \frac{1}{Q_{t}\cdot T_{n}}\frac{dn}{dt}&=&(n_{\infty}(v)-n)/{t_{n}(v)} \end{array} $$

(8b)

$$\begin{array}{@{}rcl@{}} \frac{1}{Q_{t}\cdot T_{h}}\frac{dh}{dt}&=&(h_{\infty}(v)-h)/{t_{h}(v)} \end{array} $$

(8c)

$$\begin{array}{@{}rcl@{}} \frac{\sigma}{Q_{t}\cdot P_{\max}\cdot K_{Ca}}\frac{dc}{d\tau}&=& (\bar{L}_{{\text{IP}}_{3}}+\bar{P}_{{\text{IP}}_{3}}G^{3}(c) l^{3})\\ &&\times(\bar{[Ca]}_{\text{Tot}}-c-\sigma\cdot c)\\ &&-\bar{g}_{\text{SERCA}}(c)\cdot c \end{array} $$

(8d)

$$\begin{array}{@{}rcl@{}} \frac{1}{Q_{t}\cdot Q_{c}\cdot A}\frac{dl}{d\tau}&=& \bar{K}_{\mathrm{d}}(1-l)-c l\ \end{array} $$

(8e)

with dimensionless parameters $\bar {L}_{{\text {IP}}_{3}}=L_{{\text {IP}}_{3}}/P_{\max }$, $\bar {P}_{{\text {IP}}_{3}}(c)=P_{{\text {IP}}_{3}}/P_{\max }$, $\bar {g}_{\text {SERCA}}(c)=g_{\text {SERCA}}([\text {Ca}])/P_{\max }$ and $\bar {K}_{\mathrm {d}}=K_{\mathrm {d}}/Q_{c}$ .

Since we expect V∈[−60,20] and [Ca]∈[0,1], suitable choices for the voltage and calcium scales are Q _v =100 mV and Q _c =1 μM, respectively. We also see that values of m _∞ (V), m p _∞ (V), f([Ca]), n _∞ (V), h _∞ (V), G([Ca]), $\bar {g}_{\text {SERCA}}([\text {Ca}])$, n, h and l all lie in the range [0,1]. For the choice of parameters specified in Table 1, the maximum conductance is g _Na=28 nS, so we have g _max=g _Na. Numerical evaluations of 1/τ _n (V) and 1/τ _h (V) for V∈[−60,20] show that T _n ≈20 ms⁻¹ and T _h ≈0.04 ms⁻¹. Similarly, we obtain G _c ≈0.0421 and G _S ≈1000 pL⋅m s ⁻¹, so we have P _max≈1305 pL⋅m s ⁻¹. Using these values we see that all terms in the right hand sides of Eqs. (8a)–(8e) are bounded (in absolute value) by one.

The coefficients of the derivatives in the left hand sides of Eqs. (8a)–(8e) now reveal the relative rates of evolution of the variables. We find that C _m /g _max=0.75 ms∼O(1) m s, 1/T _n =0.05 ms∼O(0.1) ms, 1/T _h =25ms∼O(10) m s, $\frac {\sigma }{P_{\max }\cdot K_{Ca}} = 5.67 \,\text {ms}\sim O(10)\, ms$ and $\frac {1}{Q_{c}\cdot A} = 200 \,\text {ms} \sim \, O(100)\, ms$. We choose the fast timescale as our reference time, i.e., pick Q _t =1 ms, and set

$$\begin{array}{@{}rcl@{}} &&R_{v}:=\frac{C_{m}}{Q_{t}\cdot g_{\max}},\qquad\qquad R_{x}:=\frac{1}{Q_{t}\cdot T_{x}}\,, \ x\in\{n, h\}, \\ \end{array} $$

(9a)

$$\begin{array}{@{}rcl@{}} &&R_{c}:=\frac{\sigma}{Q_{t}\cdot P_{\max}\cdot K_{Ca}},\qquad\!\!\!\!\! R_{l}:=\frac{1}{Q_{t}\cdot Q_{c}\cdot A}\,. \end{array} $$

(9b)

As a result, the dimensionless system (8a) becomes the system (4a) given in Section 3, namely

$$\begin{array}{@{}rcl@{}} R_{v}\frac{dv}{d\tau}&=&-\bar{g}_{\mathrm{L}}(v-\bar{V}_{\mathrm{L}})-\bar{g}_{\mathrm{K}}n^{4}(v-\bar{V}_{\mathrm{K}})\\&&-\bar{g}_{\text{Na}}m_{\infty}^{3}(v)(1-n)(v-\bar{V}_{\text{Na}})\\ &&-\bar{g}_{\text{NaP}}mp_{\infty}(v)h(v-\bar{V}_{\text{Na}})\\ &&-\bar{g}_{\text{CAN}}f(c)(v-\bar{V}_{\text{Na}}):=f_{1}(v,\,n,\,h,\,c) \end{array} $$

(10a)

$$\begin{array}{@{}rcl@{}} R_{n}\frac{dn}{d\tau}&=&(n_{\infty}(v)-n)/{t_{n}(v)}:=g_{1}(v,\,n)/{t_{n}(v)} \end{array} $$

(10b)

$$\begin{array}{@{}rcl@{}} R_{h}\frac{dh}{d\tau}&=&(h_{\infty}(v)-h)/{t_{h}(v)}:=h_{1}(v,\,h)/{t_{h}(v)} \end{array} $$

(10c)

$$\begin{array}{@{}rcl@{}} R_{c}\frac{dc}{d\tau}&=& (\bar{L}_{{\text{IP}}_{3}}+\bar{P}_{{\text{IP}}_{3}}G^{3}(c) l^{3})(\bar{[Ca]}_{\text{Tot}}-c-\sigma\cdot c)\\&&-\bar{g}_{\text{SERCA}}(c)\cdot c :=f_{2}(c,\,l) \end{array} $$

(10d)

$$\begin{array}{@{}rcl@{}} R_{l}\frac{dl}{d\tau}&=& \bar{K}_{\mathrm{d}}(1-l)-c l:=g_{2}(c,\,l)\ \end{array} $$

(10e)

where R _v , R _n , R _h , R _c and R _l are dimensionless parameters given in (9a).