A Model for Fluid Drainage by the Lymphatic System

Abstract

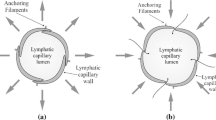
This study investigates the fluid flow through tissues where lymphatic drainage occurs. Lymphatic drainage requires the use of two valve systems, primary and secondary. Primary valves are located in the initial lymphatics. Overlapping endothelial cells around the circumferential lining of lymphatic capillaries are presumed to act as a unidirectional valve system. Secondary valves are located in the lumen of the collecting lymphatics and act as another unidirectional valve system; these are well studied in contrast to primary valves. We propose a model for the drainage of fluid by the lymphatic system that includes the primary valve system. The analysis in this work incorporates the mechanics of the primary lymphatic valves as well as the fluid flow through the interstitium and that through the walls of the blood capillaries. The model predicts a piecewise linear relation between the drainage flux and the pressure difference between the blood and lymphatic capillaries. The model describes a permeable membrane around a blood capillary, an elastic primary lymphatic valve and the interstitium lying between the two.

Appendices

Appendix A: Interstitial Fluid Flux Between a Blood and Lymphatic Capillary

1.1 A.1 Problem Formulation

The purpose of this section is to find an expression for the fluid flux per unit length through the interstitium. For Cases 1 and 2 (a closed lymphatic valve), there is no fluid flow into the lymphatic capillary (∂P/∂n=0 on the exterior of the lymphatic valve) and, therefore, no fluid flow through the blood capillary wall since our model does not include tissue expansion. A very trivial solution to Cases 1 and 2 for the fluid flow through the interstitium is $P=\widehat {P}$, making ∂P/∂n=0 on the wall of the blood capillary. For the rest of this section, we investigate Case 3, an open lymphatic valve. Darcy’s law, $\mathbf{u} = -\frac{\kappa}{\mu}\nabla P$, characterizes the fluid flow in the interstitium. Assuming the fluid is incompressible, ∇.u=0, and κ/μ is constant, reveals Laplace’s equation when we take the divergence of Darcy’s law,

$$ \nabla^{2}P=0. $$

(19)

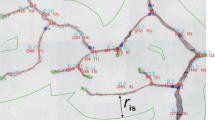
Figure 10 displays the complex domain in which Laplace’s equation is to be solved as well as all the boundary conditions. The periodic tile now has non- circular boundaries for the capillaries because we believe polygonal boundaries are sufficient in representing the morphology of capillaries, and in addition this simplifies the analysis later on. Since Laplace’s equation holds under conformal mapping, we use a transformation technique to simplify our domain.

Fig. 10

A cross-sectional view of the interstitium

The dotted lines in Fig. 10 are where we impose a constant pressure. The pressure profile near the blood capillary was calculated in Sect. 2.3, which demonstrates constant pressure of the form $P_{b}=(\widehat{P}\pi\alpha r_{b}+2\xi P_{l})/(\pi\alpha r_{b} + 2\xi)$ on the blood capillary wall.

1.2 A.2 A Conformal Mapping Approach for the Interstitial Fluid Flux

The conformal map used in this section is the Schwarz Christoffel’s transformation (SC). We have described the SC transformation in detail since we believe it is useful to understand how the transformation works and how we interpret the transformation for our model. Schwarz Christoffel’s transformation is a conformal map of the upper half-plane onto the interior of a polygon.

Mapping to the periodic tile from the upper half plane can be accomplished by using the Schwarz Christoffel transformation formula. Solving Darcy’s law in the upper half plane is less challenging than inside the polygonal area. However, we can still simplify the “new” domain further; a square or a rectangle would suffice since we could engineer it to have only one boundary condition on each side. Therefore, the two maps that we will investigate are: a transformation from a rectangle to the upper half plane, and another transformation from the upper half plane to the periodic tile (the original domain).

The method behind the Schwarz Christoffel transformation is that a conformal transformation f may have a derivative that can be expressed as

for certain functions f _m .

We assume that a polygon has vertices q ₁,…,q _n and interior angles ϑ ₁ π,…,ϑ _n π in counterclockwise order, and let f be any conformal map from the upper half-plane to the interior of the polygon with f(±∞)=q _n . Then the Schwarz Christoffel formula for a half-plane is

$$ f(z)=A +C\int^{z}\prod_{m=1}^{n-1}( \zeta-z_{m})^{\vartheta_{m}-1}d\zeta, $$

(20)

for some complex constants A and C, where q _m =f(z _m ). Derivation of this formula uses the method of the Schwarz reflection principle (Driscoll and Trefethen 2002). The exponents in the integrand in Eq. (20) induce the correct angles in the image of the half-plane, regardless of where the prevertices lie on the polygon. In order to map to a given target, we determine the locations of the prevertices by enforcing conditions involving the side lengths,

$$ \frac{\vert \int^{z_{m+1}}_{z_{m}}f'(\zeta)\,d\zeta \vert }{\vert \int^{z_{2}}_{z_{1}}f'(\zeta)\,d\zeta \vert }=\frac{\vert q_{m+1}-q_{m}\vert }{\vert q_{2}-q_{1}\vert }, $$

(21)

where m=2,…,n−2 (Driscoll and Trefethen 2002). This formula produces simultaneous equations where one can confidently solve if good starting values are known.

The Schwarz Christoffel mapping integral below maps from the upper half-plane to the polygon (the original domain).

$$ \varPhi=f(z)=\int_{0}^{z}\frac{(\zeta-c)^{\frac{1}{4}}(\zeta-d)^{\frac {1}{4}}(\zeta+k)^{\frac{1}{4}}(\zeta+l)^{\frac{1}{4}}}{(\zeta-a)^{\frac {1}{2}}(\zeta-b)^{\frac{1}{2}}(\zeta-e)^{\frac{1}{2}}(\zeta+h)^{\frac {1}{2}}(\zeta+p)^{\frac{1}{2}}}\,d \zeta, $$

(22)

with a=0 μm, b=0.1 μm, c=0.1006 μm, d=0.1023 μm, e=0.103 μm, h=−0.148 μm, k=−0.151 μm, l=−0.156 μm, p=−0.159 μm being the prevertices on the real axis. Only the ratio between each prevertex not the magnitude creates our desired domain. Using the conditions on the side lengths, (21), the prevertices are comfortably determined. Figure 11 shows where each prevertex transforms to in our polygon, for the transformation from a rectangle to the upper half-plane needs the inversion of the Schwarz Christoffel formula (20). To decipher the inverse of this formula is difficult, because in general no formula exists (Driscoll and Trefethen 2002). The two main strategies for inversion are Newton iteration on the forward map f(z)−q=0, and a numerical solution of the initial value problem,

$$ \frac{dz}{dq}=\frac{1}{f'(z)},\qquad z(q_{0})=z_{0}. $$

(23)

Fig. 11

The SC transformation from the upper half-plane to the polygon

The Newton iteration method is attractive because f′(z) is known. However, in practice one may need a rather good starting guess to avoid divergence. Solving the initial value problem, on the other hand, is more reliable, but considerably slower (Driscoll and Trefethen 2002).

By using Jacobian elliptic functions, we can invert the SC formula for the transformation from the upper half-plane to a rectangle, in this case, the Jacobian elliptic sine function. The Schwarz Christoffel formula for a map to a rectangle is

(24)

For the sake of argument, we assume the complex constants to be $\overline{A}=0$ and $\overline{C}=1$, because we have no preference where and how large the rectangle is in the complex v-plane. If we had a symmetrical polygon (the diameter of the blood and lymphatic capillaries are the same, i.e., b=−k and e=−l), the inverse of (24) would become simple because we can change the variable of the mapping function by ζ=sinθ, which results directly to the Jacobi elliptic sine function. However, the sizes of the blood and lymphatic capillaries are different, so a different approach is required. To acquire the inverse, we need to integrate (24) before inverting. Integrating (24) acquires

(25)

which simplifies to

$$ W = \left\{ \begin{array}{l@{\quad } l} \frac{2}{\sqrt{b-k}\sqrt{e-l}}\mbox{EllipticF} \bigl(\sqrt{\frac {(b-k)(\varPhi-l)}{(b-l)(\varPhi-k)}},\sqrt{\frac {(e-k)(b-l)}{(e-l)(b-k)}} \bigr) & \mbox{if}\ l<\varPhi<k, \\[6pt] \frac{-2}{\sqrt{b-k}\sqrt{e-l}}\mbox{EllipticF} \bigl(\sqrt{\frac {(b-k)(\varPhi-l)}{(b-l)(\varPhi-k)}},\sqrt{\frac {(e-k)(b-l)}{(e-l)(b-k)}} \bigr) & \mbox{if}\ l>\varPhi>k. \\ \end{array} \right. $$

(26)

This inverts to

$$ \varPhi= \left\{ \begin{array}{l @{\quad }l} \frac{l-k\frac{b-l}{b-k}\mbox{JacobiS} (\frac{\sqrt {b-k}\sqrt{e-l}}{2}W,\sqrt{\frac{(e-k)(b-l)}{(e-l)(b-k)}} )^{2}}{1-\frac {b-l}{b-k}\mbox{JacobiS} (\frac{\sqrt{b-k}\sqrt{e-l}}{2}W,\sqrt{\frac {(e-k)(b-l)}{(e-l)(b-k)}} )^{2}} & \mbox{if}\ l<\varPhi<k, \\\noalign{\vspace{4pt}} \frac{l-k\frac{b-l}{b-k}\mbox{JacobiS} (-\frac{\sqrt{b-k}\sqrt {e-l}}{2}W,\sqrt{\frac{(e-k)(b-l)}{(e-l)(b-k)}} )^{2}}{1-\frac {b-l}{b-k}\mbox{JacobiS} (-\frac{\sqrt{b-k}\sqrt{e-l}}{2}W,\sqrt{\frac {(e-k)(b-l)}{(e-l)(b-k)}} )^{2}} & \mbox{if}\ l>\varPhi>k, \\ \end{array} \right. $$

(27)

where w are points in the rectangle. Therefore, we now have a map to our polygon from a rectangle via the upper half-plane. Figure 12 shows where each prevertex transforms to in the upper half-plane. The vertices on the rectangle are w ₁=0 μm, w ₂=100.06 μm, w ₃=30.26ı μm, w ₄=100.06+30.26ı μm map to l, e, k, c, respectively.

Fig. 12

The SC transformation from a rectangle to the upper half-plane

Solving Laplace’s equation inside the rectangle to acquire the stream-lines of the flow is now become trivial because we have assumed that the pressure is approximately constant on the wall of the blood capillary. Using separation of variables on Laplace’s equation leads to

$$ P=\frac{P_{l}-P_{b}}{w_{2}}u+P_{b}. $$

(28)

The instantaneous discharge rate through the interstitium, Q, is

$$ Q=\xi\frac{\kappa}{\mu}(P_{b}-P_{l}), $$

(29)

where ξ corresponds to the height divided by the length of the rectangle in Fig. 12, which represents the interstitial space (0.302).

Figure 13 graphically demonstrates the Schwarz Christoffel transformation from a rectangle to the upper half-plane. The stream-lines in each region are plotted in Maple.

Fig. 13

Solution in rectangle mapped to our polygon via the upper half-plane by the Schwarz Christoffel integral equations

An initial glance at the solution concurs that the SC mapping technique was a success in predicting the fluid flow. The accuracy of our analytical solution is compared by a numerical solution from a finite element package, Comsol Multiphysics. Figure 14 compares the numerics to the analytics and as you can see they are very similar.

Fig. 14

(1) Stream-lines of the fluid flow in the interstitium plotted in Comsol

Appendix B: The Interstitial Flux as a Function of Pressure Difference for Small Vessels

2.1 B.1 Problem Formulation

Here, we derive an asymptotic expression for the interstitial flux Q as a function of the pressure difference between the outer edge of the blood capillary and the outer edge of the lymphatic capillary. Since the vessel radii are small in comparison to the separation between their centers $\sqrt{L_{x}^{2}+L_{y}^{2}}$, we can accurately approximate the pressure on the surface of each vessel as a constant, denoting that on the blood capillary by P _b and that on the lymph capillary by P _l .² Having made this approximation and on defining r=(x ²+y ²)^1/2 and  $\widehat{r}=((x-L_{x})^{2}+(y-L_{y})^{2})^{1/2}$ the problem for the flow in the interstitial medium Ω becomes

(30)

(31)

where r _b and r _l are the radii of the blood capillary and the lymph vessel, respectively. The flow, from the edge of the blood capillary r=r _b to the edge of the lymph capillary $\widehat{r}=r_{l}$, has a total flux Q which can be evaluated from either of the two expressions

(32)

where θ and ϕ are the azimuthal angles about the blood capillary and the lymph capillary, respectively.

In order to proceed further with the asymptotic treatment of this problem it is necessary to nondimensionalize the problem, which we do by writing x=L _x x′, P=(P _b +P _l )/2+p ^∗ P′, and Q=(κp ^∗/μ)Q′ where primes denote dimensionless variables. On defining the dimensionless parameters

(33)

and choosing the pressure scaling p ^∗=(P _b −P _l )/(2log(1/ϵ)) this leads to the following dimensionless form of the problem

(34)

(35)

with the flux conditions

(36)

Henceforth, we drop the primes from the dimensionless variables

2.2 B.2 Asymptotic Analysis in the Limit ϵ≪1

We now analyze the dimensionless problem (34)–(36) in the limit that ϵ≪1 and the other parameters, λ and H, are order one. Our aim here is to derive an (approximate) expression for Q the flux from the blood capillary to the lymphatic capillary. We start by analyzing the flow in the narrow boundary layer regions, of width O(ϵ), about the blood capillary (which we denote region I) and about the lymphatic capillary (which we denote region II).

2.2.1 B.2.1 Region I (Boundary Layer About Blood Capillary)

Here, we rescale distance from the center of the capillary with ϵ by writing r=ϵR so the that governing equations and boundary conditions (derived from (34)–(36)) become

(37)

(38)

(39)

Motivated by the form of this problem, we expand P and Q as follows:

Such logarithmic expansions of the pressure occur in a similar problem for oxygen consumption in a tissue supplied by a series of parallel capillaries (Titcombe and Ward 2000), and as here, the expansion can be summed to give an asymptotic expansion for the interstitial flux which is correct up to O(ϵ). Substituting the above expansion into (37), solving for $P^{(I)}_{n}$ (for n=1,2,…), applying the boundary conditions (38) and relating the remaining undetermined constant in the solution to the flux via (39) gives³

(40)

2.2.2 B.2.2 Region II (Boundary Layer About Lymphatic Capillary)

Here, we rescale distance from the center of the capillary with ϵ by writing $\widehat{r}=\epsilon\rho$ so the that governing equations and boundary conditions (derived from (34)–(36)) become

(41)

(42)

(43)

Here, we expand P as follows:

Substituting the above expansion into (41), solving for $P^{(II)}_{n}$ (for n=1,2,…), applying the boundary conditions (42) and relating the remaining undetermined constant in the solution to the flux via (43) gives

(44)

2.2.3 B.2.3 Outer Region

In the outer region between the capillaries, we solve the following problem for the pressure

(45)

(46)

and obtain conditions on P as x ²+y ²→0 and as (x−1)²+(y−λ)²→0 by matching to the solution in regions I and II, respectively.

2.2.4 B.2.4 Matching Between Inner Regions (I) and (II) and the Outer

In order to match from regions (I) and (II) to the outer, we write the asymptotic solution in (I) in terms of outer variables as R→∞

(47)

and that in (II) in terms of outer variables as ρ→∞

(48)

2.2.5 B.2.5 Outer Region

Returning to the outer it becomes apparent from the matching conditions (47)–(48) that the expansion for P ^(o) proceeds as follows:

$$ P^{(o)}=P^{(o)}_0+\frac{1}{\log(1/\epsilon)} P^{(o)}_1+\frac{1}{\log^2(1/\epsilon)} P^{(o)}_2+ \cdots+\frac{1}{\log^n(1/\epsilon)} P^{(o)}_n+\cdots $$

(49)

and that

(50)

The matching conditions on the nth term of this expansion for the pressure, arising from (47)–(48), are

$$ \left . \begin{array} {l@{\quad }l} \displaystyle P^{(o)}_n \sim-\frac{2}{\pi} \bigl( Q_n (\log r +\log H)+Q_{n+1} \bigr) & \mbox{as}\ r \rightarrow0 \\ \displaystyle P^{(o)}_n \sim\frac{2}{\pi} \bigl( Q_n (\log\widehat{r} -\log H)+Q_{n+1} \bigr) & \mbox{as}\ \widehat{r} \rightarrow0 \end{array} \right \}\quad \mbox{for}\ n=0,1,2, \ldots $$

(51)

where r=(x ²+y ²)^1/2 and $\widehat{r}=((x-a)^{2}+(y-\lambda)^{2})^{1/2}$. On substituting the expansion (49) into (45)–(46), taking the O(log⁻ⁿ(1/ϵ)) term (for n=0,1,2,…) and accounting for the logarithmic singularities in the matching conditions (51), we obtain the following problem for $P^{(o)}_{n}$:

(52)

(53)

We solve this problem using separation of variables to find

(54)

(55)

where c ₁ is a constant that can be determined uniquely by matching to the inner regions. The other constants in the solution are defined by

(56)

(57)

(58)

(59)

(60)

This solution for $P^{(o)}_{0}$ is plotted in Fig. 15.

Fig. 15

The pressure profile in the periodic tile

2.2.6 B.2.6 Solvability Conditions on the Flux

The fluxes Q _n can be determined by matching the solution found in (55), to region (I), as r→0, and to region (II), as $\widehat{r} \rightarrow0$. The formulation of the problem in (52) accounts only for the logarithmic singularities in the matching conditions (51a)–(51b). And, in order to complete the matching to regions (I) and (II), we need to ensure

(61)

(62)

By subtracting (61) from (62), referring to (54) and defining the constants K ₁ and K ₂ by

we obtain a recursion relation between subsequent terms in the flux expansion

(63)

On recalling that Q ₀ is given in (50), we obtain the following expression for Q _n

(64)

and consequently the following geometric series for the leading order terms in the expansion of Q:

Summing this series gives an expression for the dimensionless flux (we replace the primes to avoid confusion with the dimensional result)

(65)

Redimensionalizing this, we obtain

(66)

2.2.7 B.2.7 Evaluation of Q for a Square Lattice

Given a square lattice of lymphatic and blood capillaries arranged in a checkered pattern with separation between adjacent vessels of S so that $L_{x}=L_{y}=S/\sqrt{2}$. It follows that λ=1 and ϵ=(2r _b r _l )^1/2/S. Evaluating (K ₁−K ₂) with λ=1, we find K ₁−K ₂=2.654.

Appendix C: Derivation of the Nonlinear Beam Equation

We describe the valve deformation using arc length s along the beam and the angle θ(s) between the beam and the x-axis, as shown in Fig. 16a, and assume the beam to be inextensible, so that its the arc-length is conserved by the deformation (Howell et al. 2009). The transverse displacement is given parametrically by x=x(s), y=y(s), where

$$ \frac{\mathrm{d} x}{\mathrm{d} s}=\cos\theta,\qquad \frac {\mathrm{d} y}{\mathrm{d} s}=\sin\theta. $$

(67)

Fig. 16

(a) A geometrical view of the lymphatic valve. (b) The forces acting on a small section of the lymphatic valve

To obtain the nonlinear loaded beam equation, we first consider a small element of the lymphatic valve of length ds, and derive the equations that govern the balance of forces and moments on this element. The element is held under tension T at each end. A force F  ds is applied in the direction normal to the valve, with a tangential component, G  ds. M is the bending moment at each end of the valve and N is the normal force at the ends of the valve (Howell et al. 2009). The forces acting on the lymphatic valve are summarized in Fig. 16b.

By carrying out a force balance in the standard fashion, we obtain an expression for the resultant forces acting in the x and y directions. Since damping forces are large we assume a quasistatic configuration in which the resultant forces are both zero, so that

(68)

(69)

Using the product rule to expand the above equations, multiplying (68) by cos(θ) and adding it to (69) multiplied by sin(θ), leads to

$$ \frac{dT}{ds}-N\frac{d\theta}{ds}=-G. $$

(70)

Similarly, taking the product of (68) with sin(θ) and adding this to the product of (69) and cos(θ), gives

$$ \frac{dN}{ds}+T\frac{d\theta}{ds}=-F. $$

(71)

In order to derive a moment balance equation, we assume that the infinitesimal section of the lymphatic valve (see Fig. 16b) is approximately straight and length ds. Balancing moments about the left-hand point of the valve in Fig. 16b, gives

$$ N=-\frac{dM}{ds}. $$

(72)

As a constitutive relation, we expect the bending moment (M) to be proportional to the valve curvature, which is given by dθ/ds. Since we consider small strains in the geometrically nonlinear beam, we assume that the constant of proportionality is the same as in a linear case, that is,

$$ M=D\frac{d \theta}{d s}, $$

(73)

where D (kg μm² s⁻²) is the flexural rigidity of the valve. We use plate theory to describe the flexural rigidity of the lymphatic valve in terms of the Young’s modulus (E), the Poisson’s ratio (ν) and the beam thickness (ι) by D=Eι ³/12(1−ν ²).

We seek an equation that only depends on the angle θ and the arc length s. To achieve this we eliminate N, T and M from the force balance equations (70)–(73) and equate F, the normal force acting on the lymphatic valve, with the pressure drop across the initial lymphatics, P _l −P ₀. Assuming the no slip boundary condition on the exterior of the lymphatic valve (no shear force) results in the tangential force G applied on the valve to be zero. It follows that

$$ \frac{\mathrm{d}^{3}\theta}{\mathrm{d} s^{3}}+\frac{1}{2} \biggl(\frac {\mathrm{d}\theta}{\mathrm{d} s} \biggr)^{3}=\frac{P_{l}-P_{0}}{D}. $$

(74)

Equation (74) is the Euler–Bernoulli beam equation for large deformations in terms of angle and arc-length.