In-medium properties of pseudoscalar $D_s$ and $B_s$ mesons

Abstract

We calculate the shift in the masses and decay constants of $D_s(1968)$ and $B_s(5370)$ mesons in hot and dense asymmetric strange hadronic matter using QCD sum rules and chiral SU(3) model. In-medium strange quark condensates $\left\langle \bar{s}s\right\rangle _{\rho _B}$, and gluon condensates $\left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu } \right\rangle _{\rho _B}$, to be used in the QCD sum rules for pseudoscalar $D_s$ and $B_s$ mesons, are calculated using a chiral SU(3) model. As an application of our present work, we calculate the in-medium decay widths of the excited ($c\bar{s}$) states $D_s^*(2715)$ and $D_s^*(2860)$ decaying to ($D_s(1968),\eta$) mesons. The medium effects in their decay widths are incorporated through the mass modification of the $D_s(1968)$ and $\eta$ mesons. The results of the present investigation may be helpful in understanding the possible outcomes of the future experiments like CBM and PANDA under the FAIR facility.

1 Introduction

Exploring the QCD phase diagram at different temperatures and baryon chemical potentials is an interesting and challenging problem. The heavy-ion collision experiments e.g., RHIC and LHC are intended to probe the phases of QCD at a region of high temperature and low baryonic density. However, future facilities like CBM and PANDA of the FAIR project (at GSI Germany) are expected to explore the QCD phases at a region of high baryonic density and moderate temperature. The possibility of the production of open charm in these heavy-ion collision experiments and also in the J-PARC facility encourages us to investigate heavy mesons in nuclear matter [1, 2]. In particular, the study of the open charm and bottom mesons in nuclear as well as in strange hadronic matter can highlight the important points of the yields of $J/\psi$ and $\Upsilon$ states produced in the heavy-ion collision experiments. It was first predicted by Matsui and Satz [3] that the decrease in the yield of the $J/ \psi$ state in the medium should be considered as a signature of the production of a quark gluon plasma in HIC experiments. In Ref. [4] the authors observed drastic change in the effective spectrum of vector channel $J^P=1^{++}$ at temperature interval $\simeq$ 150–200 MeV, in hadronic matter. Also, using a sum rule approach with conservative stability criteria, the authors did not observe drastic effects of dynamical fermions on the phase transitions in QCD [5]. Furthermore, in Refs. [6, 7] the authors observed the survival of $\eta _c$ and $\chi _c ( \Upsilon$ and $\eta _b$) states beyond the critical temperature $T_c$. On the other hand, the $\chi _b$ and $h_b$ states were observed to melt in the QGP phase in [8].

Moreover, experimental evidence of $J/\psi$ suppression was observed by the NA38 [9], NA50 [10] and NA60 [11] collaborations. The results in favour of $J/\psi$ suppression were also observed in the RHIC experiment [12], whereas the decrease in the yield of hidden bottom mesons ($\Upsilon (1S), \Upsilon (2S)$, etc.) was observed in the Pb–Pb collisions of the LHC experiment [13]. However, in [14,15,16], the authors claimed that the in-medium modification of the D meson can also alter the yield of $J/\psi$ in the HIC experiments. One expects that if the masses of the D(B) mesons decrease in the medium then the higher charmonium (bottomonium) states may decay to D(B) mesons instead of $J/\psi$ ($\Upsilon$) and hence this may decrease the yield of $J/\psi$ ($\Upsilon$) in the hadronic medium as well. Therefore, to avoid an erroneous consideration of the hadronic phase as QGP phase, the in-medium study of D and B mesons becomes important. In addition to $J/ \psi (\Upsilon )$ suppression, study of D(B) mesons in a hadronic medium may also reveal the existence of bound states of D(B) mesons with nucleons [17], as well as of hyperons [18]. Furthermore, to understand the results of enhanced production of D and $\bar{D}$ mesons in antiproton–nucleon collisions, the study of in-medium properties of D mesons is important [19, 20]. A detailed recent review on the study of experimental and theoretical progress of open charmed and bottom mesons can be found in Ref. [21].

The study of ground states $D_s (c\bar{s})$ and $B_s (\bar{b}s$) mesons in hot and dense asymmetric hadronic matter may help to understand the in-medium interactions of light and heavy quarks, and this furthermore may also explain the diffusion and hadronisation by the efficacy of strangeness enhancement in the ultrarelativistic heavy-ion collision experiments [22, 23]. Also, the comparison of elliptic flow of the in-medium strange $D_s$ mesons with the non-strange D mesons may help to analyse quantitatively the hadronic transport coefficients, and this furthermore helps in gaining a quantitative understanding of the viscosity to entropy ratio in hadronic matter [23]. Furthermore, knowledge of the in-medium properties of the $D_s$ and $B_s$ mesons helps to understand the in-medium leptonic decay constants and this may further lead to the understanding of the heavy flavour electroweak transition and CP violation. In the chiral limit, we have $\frac{f_{D_s}}{f_{D}}=1$ and $\frac{f_{B_s}}{f_{B}}=1$, and when chiral symmetry breaks, the ratios deviate from unity [24,25,26,27,28]. For example, using lattice QCD, the ratios were predicted as $\frac{f_{D_s}}{f_{D}}=1.188$ and $\frac{f_{B_s}}{f_{B}}=1.229$ [27]. Similarly, in [28], the value of $\frac{f_{D_s}}{f_{D}}$ was observed to be 1.187. Here we point out that the in-medium decay constants of the $D_s/B_s$ and D / B mesons may behave differently in the hadronic medium and therefore it will be of interest for understanding the extent of the flavour symmetry breaking effect in future heavy-ion collision experiments. Recently, an enhanced ratio $\frac{D_s^+}{D^0}$ was measured in Au–Au collisions at $\sqrt{s_{NN}}=200$ GeV in the STAR experiment [29].

Theoretically, many methodologies have been developed to study the in-medium D and B mesons, giving different results. For example, in Ref. [17], the authors observed a drop of the mass of D meson using the Quark Meson Coupling Model (QMC), in which quarks and gluons are degrees of freedom, and interactions between D mesons and nucleons are considered through the exchange of scalar and vector mesons. Another approach is by the self-consistent coupled channel, which considers the hadrons as degrees of freedom [30]. This approach was further modified from SU(3) flavour [30] to SU(4) and breaking of the SU(4) symmetry via exchange of vector mesons [18, 31]. Using this approach the authors calculated a positive shift in the mass of D mesons [32], whereas a negative shift in the mass of the $D_s$ mesons in strange hadronic matter was observed [18, 33, 34].

On the other hand, in the QCD sum rules, an operator product expansion (OPE) is applied on the current–current correlation function and a Borel transformation is used to equate the mass dependent terms and the various condensates up to dimension four [35], further modified to dimension five [36]. Using the linear density approximate QCD sum rules, the authors separated the even and odd terms of the correlation function to evaluate the mass splitting between D and $\bar{D}$ mesons, as well as between $D_s$ and $\bar{D_s}$ mesons [36]. In [37] using QCD sum rules and chiral SU(3) model, we evaluated the in-medium masses and decay constants of vector and axial vector $D_1$ and $B_1$ mesons, and observed repulsive interaction for axial vector whereas, attractive interaction for vector $D^*$ and $B^*$ mesons in hadronic medium [37]. Recently, in Ref. [38] the authors used the Gaussian transformed QCD sum rules with maximum entropy method to calculate the mass splitting between D and $\bar{D}$ mesons, followed by the Bayesian approach [39]. Another model based on the chiral SU(3) symmetry had been widely used in the past to calculate in-medium mass of hadrons [40] and properties of the neutron stars [41]. In [42] the authors observed a decrease in the mass of light vector mesons including the baryon Dirac sea, through the summation of baryon tadpole diagram in the relativistic Hartree approximation. Using the chiral SU(3) model the authors studied the masses and optical potential of kaons and antikaons in nuclear matter [43, 44] and in hyperonic matter [45]. To observe the behaviour of open charmed and bottom mesons in nuclear matter the SU(3) model was generalised to the SU(4) and SU(5) sectors, and a negative shift in the masses of the D and B mesons was observed [46,47,48]. In [49, 50], the authors used the same approach of generalising the SU(3) model to SU(4), in order to investigate the interaction of the $D_s$ and $B_s$ mesons, in asymmetric strange hadronic matter at finite temperature. Using this approach the authors calculate the attractive interaction of the $D_s/B_s$ mesons in hot and dense asymmetric hyperonic (along with the nucleons) medium.

In the present investigation, we apply the chiral SU(3) model followed by the QCD sum rules approach, to calculate the shift in masses and decay constants of pseudoscalar strange charmed ($D_s$) and bottom ($B_s$) mesons in strange hadronic matter. We first calculate the strange quark condensates $\left\langle \bar{s}s\right\rangle$, and gluon condensates $\left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu } \right\rangle$, in hot and dense asymmetric hadronic matter through a chiral SU(3) model, and then we use these condensates as input in the Borel transformed QCD sum rules to find the medium modified masses and decay constants for the $D_s$ and $B_s$ mesons. Furthermore, as an application of the mass modification of the $D_s(1968)$ meson, we investigate the in-medium two mode partial decay width of the $D_s^*(2715)$ and $D_s^*(2860)$ states decaying to ($D_s(1968),\eta$) mesons, using the $^3 P_0$ model. Additionally, we introduce the in-medium mass of the $\eta$ meson, calculated using the heavy-baryon chiral perturbation model along with relativistic mean field theory [51].

The $^3P_0$ model had been applied in the past to compute the values of two body strong decay widths of various mesons [52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67]. Two states $D_s^*(2715)$ and $D_s^*(2860)$ are of particular importance having recently been predicted by the Belle and Babar collaborations, with full decay widths nearly $\Gamma = 115$ and 48 MeV, respectively. However, the clear cut assignment of the quantum numbers is still not uniquely confirmed. Theoretically, the authors had observed various decay modes (in vacuum) of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons to judge their exact quantum numbers. For example, in Refs. [59, 65, 68,69,70], the authors used the $^3P_0$ model to investigate different partial decay widths of the above mentioned mesons and the authors suggested for the possible quantum numbers of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons $1^-(1^3D_1)$ and $3^-(1^3D_3)$, with the slight possibility of the states to be assigned to $1^-(2^3S_1)$ and $1^-(1^3D_1)$, respectively. As mentioned in [68], the observed decay modes of $D_s^*(2715)$ and $D_s^*(2860)$ as $D_s(1968) + \eta$ will unveil the finite possibility (though small) to assign their states to $1^-(2^3S_1)$ and $1^-(1^3D_1)$, respectively. We consider this statement of particular interest, and we try to impose the medium effects on the partial decay widths of the $D_s^*(2715)$ and $D_s^*(2860)$ states decaying to ($D_s(1968), \eta$) and we will concentrate on the possible shift in the partial decay widths.

The outline of this paper is as follows: in Sect. 2, we describe the chiral SU(3) model to calculate in-medium strange quark and gluon condensates. In Sect. 3, we discuss the QCD sum rules to investigate the in-medium masses and decay constants of the $D_s$ and $B_s$ mesons. In Sect. 4, we narrate the $^3P_0$ model, which will be used to calculate the in-medium partial decay widths of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons decaying to ($D_s(1968),\eta$). In Sect. 5, we discuss the various results of the present work and finally, in Sect. 6, we shall summarize the present work.

2 Chiral SU(3) model

The chiral SU(3) model is an effective theory based on the chiral property of the quarks $(m_u=m_d=m_s=0)$, i.e., invariance under the chiral transformation. In the chiral SU(3) model we start with the effective Lagrangian density which contains the kinetic energy term; the baryon meson interaction term, which produces the baryon mass; the self-interaction of the vector mesons, which generates the dynamical mass of the vector mesons, scalar mesons interactions, which induce the spontaneous breaking of chiral symmetry, and the explicit breaking term of chiral symmetry. It is based on the non-realisation of chiral symmetry, and the broken scale invariance with the spontaneous breaking of chiral symmetry properties [71]. In the present investigation, we use the mean field approximation to solve the effective Lagrangian density and in this scheme we replace the quantum field operator by their classical expectation values. Furthermore, from the Lagrangian density and using the Euler Lagrange equation of motion, $\frac{\partial \mathcal {L}}{\partial \phi }-\partial _\mu \left( \frac{\partial \mathcal {L}}{\partial (\partial _\mu \phi )}\right) =0$ where $\phi$ is scalar field, we obtain coupled equations of motion for the scalar fields $\sigma$, $\zeta$, $\delta$ and the scalar dilaton field $\chi$, given as [72, 73]

$$\begin{aligned}&k_{0}\chi ^{2}\sigma -4k_{1} ( \sigma ^{2}+\zeta ^{2} +\delta ^{2} )\sigma -2k_{2} ( \sigma ^{3}+3\sigma \delta ^{2} ) -2k_{3}\chi \sigma \zeta \nonumber \\&\quad -\frac{d}{3} \chi ^{4} \bigg (\frac{2\sigma }{\sigma ^{2}-\delta ^{2}}\bigg ) +\left( \frac{\chi }{\chi _{0}}\right) ^{2}m_{\pi }^{2}f_{\pi } -\sum g_{\sigma i}\rho _{i}^{s} = 0, \end{aligned}$$

(1)

$$\begin{aligned}&k_{0}\chi ^{2}\zeta -4k_{1} ( \sigma ^{2}+\zeta ^{2}+\delta ^{2} ) \zeta -4k_{2}\zeta ^{3}-k_{3}\chi ( \sigma ^{2}-\delta ^{2} )\nonumber \\&\quad -\frac{d}{3}\frac{\chi ^{4}}{\zeta }+\left( \frac{\chi }{\chi _{0}} \right) ^{2}\left[ \sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}} m_{\pi }^{2}f_{\pi }\right] -\sum g_{\zeta i}\rho _{i}^{s} = 0, \end{aligned}$$

(2)

$$\begin{aligned}&k_{0}\chi ^{2}\delta -4k_{1} ( \sigma ^{2}+\zeta ^{2}+\delta ^{2} ) \delta -2k_{2} ( \delta ^{3}+3\sigma ^{2}\delta ) +k_{3}\chi \delta \zeta \nonumber \\&\quad + \frac{2}{3} d \chi ^4 \left( \frac{\delta }{\sigma ^{2}-\delta ^{2}}\right) -\sum g_{\delta i}\rho _{i}^{s} = 0, \end{aligned}$$

(3)

$$\begin{aligned}&k_{0}\chi ( \sigma ^{2}+\zeta ^{2}+\delta ^{2} )-k_{3} ( \sigma ^{2}-\delta ^{2} )\zeta \nonumber \\&\quad + \chi ^{3}\left[ 1 +\mathrm{{ln}}\left( \frac{\chi ^{4}}{\chi _{0}^{4}}\right) \right] +(4k_{4}-d)\chi ^{3} \nonumber \\&\quad - \frac{4}{3} d \chi ^{3} \mathrm{{ln}} \Bigg ( \bigg (\frac{\left( \sigma ^{2} -\delta ^{2}\right) \zeta }{\sigma _{0}^{2}\zeta _{0}} \bigg ) \bigg (\frac{\chi }{\chi _0}\bigg )^3 \Bigg )\nonumber \\&\quad + \frac{2\chi }{\chi _{0}^{2}}\left[ m_{\pi }^{2} f_{\pi }\sigma +\left( \sqrt{2}m_{K}^{2}f_{K}-\frac{1}{\sqrt{2}} m_{\pi }^{2}f_{\pi } \right) \zeta \right] = 0, \end{aligned}$$

(4)

respectively. In the above equations, $m_K$ and $f_K$ ($m_{\pi }$ and $f_{\pi }$) denote the mass and decay constant of the $K(\pi )$ meson, respectively, and the other parameters $k_0, k_1, k_2$, $k_3$ and $k_4$ are fitted so as to reproduce the vacuum masses of $\eta$ and $\eta '$ mesons [71]. Furthermore, ${\rho _i}^s$ represents the scalar density for the ith baryon ($i=p, n, \Lambda , \Sigma ^{\pm ,0}, \Xi ^{-,0}$) and is defined as

$$\begin{aligned}&\rho _{i}^{s} = \gamma _{i}\int \frac{d^{3}k}{(2\pi )^{3}}\nonumber \\&\qquad \times \frac{m_{i}^{*}}{E_{i}^{*}(k)} \Bigg ( \frac{1}{e^{({E_i}^* (k) -{\mu _i}^*)/T}+1} + \frac{1}{e^{({E_i}^* (k) +{\mu _i}^*)/T}+1} \Bigg ), \end{aligned}$$

(5)

where ${E_i}^*(k)=(k^2+{{m_i}^*}^2)^{1/2}$ and ${\mu _i}^* =\mu _i -g_{\omega i}\omega -g_{\rho i}\rho -g_{\phi i}\phi$, are the single particle energy and the effective chemical potential for the baryon of species i, and $\gamma _i=2$ is the spin degeneracy factor. Also, $m_i^* = - g_{\sigma i} \sigma - g_{\zeta i} \zeta - g_{\delta i}\delta$ is the effective mass of the baryons in the asymmetric hadronic medium. The parameters $g_{\sigma i}$, $g_{\zeta i}$ and $g_{\delta i}$ are fitted to reproduce the vacuum baryon masses [71]. In Eq. (4) $\sigma _0$, $\zeta _0$ and $\chi _0$ denote the vacuum values of the scalar fields $\sigma$, $\zeta$ and $\chi$. The parameter d is a constant having value 2 / 11, determined through the QCD beta function at one loop level for three colors $N_c$ and three flavours $N_f$ [71]. For given density $\rho _B$ of the baryonic medium, we solve coupled equations of motion of scalar fields using mean field approximation for the different values of strangeness fractions $f_s$, isospin asymmetric parameter I and temperature T. The strangeness fraction is defined as $f_s = \frac{\Sigma _i |s_i|\rho _i}{\rho _B}$; here $s_i$ is the number of strange quarks and $\rho _i$ is the number density of the ith baryon defined by $\rho _{i} = \gamma _{i}\int \frac{d^{3}k}{(2\pi )^{3}} ( \frac{1}{e^{({E_i}^* (k) -{\mu _i}^*)/T}+1} + \frac{1}{e^{({E_i}^* (k) +{\mu _i}^*)/T}+1})$. Furthermore, the isospin asymmetric parameter is defined as $I = -\frac{\Sigma _i I_{3i} \rho _i}{2\rho _B}$, where $I_{3i}$ is the z-component of the isospin for the ith baryon [73]. Furthermore, to evaluate the shift in the masses and decay constants of the $D_s$ and $B_s$ mesons using QCD sum rule analysis, we shall need strange quark condensate $\left\langle \bar{s}s\right\rangle$. To find this, we use the explicit chiral symmetry breaking term to represent the strange quark condensate in terms of the strange scalar field $\zeta$ as [72]

$$\begin{aligned} \left\langle \bar{s}s\right\rangle = \frac{1}{m_{s}}\left( \frac{\chi }{\chi _0} \right) ^2\left( \sqrt{2}m_K^2 f_K - \frac{1}{\sqrt{2}} m_ {\pi }^2 f_{\pi }\right) \zeta , \end{aligned}$$

(6)

here $m_s$ denotes the mass of strange quark. Also, $\chi _0$ denotes the vacuum value of the dilaton field $\chi$. To express gluon condensate in terms of the fields calculated above, we obtain the energy momentum tensor through the scale breaking term of the effective Lagrangian density. In the limit of finite quark masses, we equate the trace of the energy momentum tensor calculated in effective chiral SU(3) model with the trace of energy momentum tensor calculated in QCD, which is actually the gluon condensate [71, 73] given by

$$\begin{aligned} \left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu } \right\rangle =&\,\, \frac{8}{9} \Bigg [(1 - d) \chi ^{4} +\left( \frac{\chi }{\chi _{0}}\right) ^{2} \bigg ( m_{\pi }^{2} f_{\pi } \sigma \nonumber \\&\, + \bigg ( \sqrt{2} m_{K}^{2}f_{K} - \frac{1}{\sqrt{2}} m_{\pi }^{2} f_{\pi } \bigg ) \zeta \bigg ) \Bigg ].\quad \end{aligned}$$

(7)

This procedure helps to calculate the medium modified gluon condensates through the medium modified $\sigma$, $\zeta$ and $\chi$ fields. In the above equation, d is constant with value (2/11) and it is calculated through the one loop beta function for three flavours and colors of QCD [71].

3 QCD sum rule for $D_s$ and $B_s$ mesons

We will use the output of the chiral SU(3) model (medium modified strange and gluon condensates), as an input in the QCD sum rules to investigate the in-medium masses and decay constants of the $D_s$ and $B_s$ mesons. QCD sum is an useful technique which relate the phenomenological spectral parameters with the basic properties of QCD. In QCD sum rules we start with the two point correlation function

$$\begin{aligned} \Pi (q) = i\int d^{4}x\ e^{iq_{\mu } x^{\mu }} \langle \mathcal {T} \{J_5(x)J_5^{\dag }(0) \} \rangle _{\rho _B, T} , \end{aligned}$$

(8)

where $\mathcal {T}$ is the time-ordered covariant operator acting on pseudoscalar currents for the $D_s$ meson, represented as [74, 75]

$$\begin{aligned} J_5(x)&= J_5^\dag (x) = (m_c+m_s)\frac{\bar{c}(x)i\gamma _5 s(x)+{c}(x)i\gamma _5 \bar{s}(x)}{2} . \end{aligned}$$

(9)

For $B_s$ meson c(x) quark field will be replaced by b(x) quark field. Here, by using the above mentioned pseudoscalar current we will concentrate on the averaged shift in the masses and decay constants of the $D_s$ and $\bar{D_s}$ (Similarly for $B_s$ and $\bar{B_s}$) mesons. On the other hand, in [36], authors observed the splitting between $D_s$ and $\bar{D_s}$ mesons by separating two point correlation function into even and odd part. Furthermore, the pseudoscalar current is related to the decay constant as $\langle 0|J_5|D(k) \rangle = f_D m_D^2/(m_c+m_s)$, where D(k) is the state of D meson in four momentum k, $m_D$ and $f_D$ are the masses and decay constants of D meson, respectively [74, 75]. In the literature, using heavy quark limit, the mass of light quark is neglected as compared to the charm quark mass [35, 76]. Later on, we will point out that inclusion of the mass of strange quark will have a negligible effect on the results of this paper. Therefore, in the present calculation, we will work in the heavy quark limit, i.e., $m_c+m_s \simeq m_c$. Moreover, using the Fermi gas approximation, in the rest frame of nucleons, we decompose the two point correlation function into vacuum part, nucleon dependent part and pion bath term, i.e.,

$$\begin{aligned} \Pi (q) =\Pi _{0} (q)+ \frac{\rho _B}{2m_N}T_{N} (q) + \Pi _{P.B.}(q,T) , \end{aligned}$$

(10)

where $T_N (q)$ is the forward scattering amplitude, $\rho _B$ and $m_N$ denote the total baryon density and nucleon mass, respectively. The third term represents the thermal correlation function and is defined as [77]

$$\begin{aligned} \Pi _{P.B.}(q, T) = i\int d^{4}x\ e^{iq_{\mu } x^{\mu }} \langle \mathcal {T} \{J_5(x)J_5^\dag (0) \} \rangle _{T}, \end{aligned}$$

(11)

where $\langle \mathcal {T} \{J_5(x)J_5^\dag (0) \}\rangle _{T}$ is the thermal average of the time-ordered product of the pseudoscalar currents. The thermal average of any operator $\mathcal {O}$ is given by [77]

$$\begin{aligned} \left\langle \mathcal {O} \right\rangle _T = \frac{\mathrm{Tr} \lbrace \text {exp}\left( -H/T\right) \mathcal {O} \rbrace }{\mathrm{Tr} \lbrace \text {exp}\left( -H/T\right) \rbrace }. \end{aligned}$$

(12)

In the above $\mathrm{Tr}$ denotes the trace over complete set of states and H is the QCD Hamiltonian. The factor $\frac{\text {exp} (-H/T )}{\mathrm{Tr} \lbrace \text {exp} (-H/T ) \rbrace }$ is the thermal density matrix of QCD. In Eq. (10), the third term corresponds to the pion bath term and had been widely used in the past to consider the effect of temperature of the medium [78, 79]. We shall consider the effect of temperature through the temperature dependence of the condensates, calculated in the chiral SU(3) model and thus, we neglect the third term in Eq. (10). Furthermore, to calculate the shift in the masses and the decay constants, we express the scattering amplitude $T_N (q)$, near the pole position of the pseudoscalar mesons in terms of the spectral density [80]. This spectral density in the limit of $q \rightarrow 0$ can be further parameterized in terms of three unknown parameters a, b and c, given as [35, 81, 82],

$$\begin{aligned}&\rho (\omega ,0) \nonumber \\&\quad = -\frac{f_{D_s/B_s}^2m_{D_s/B_s}^4}{\pi m_{c/b}^2} \text{ Im } \left[ \frac{{{T}_{D_s/B_s}}(\omega ,\mathbf{0})}{(\omega ^{2}- m_{D_s/B_s}^2+i\varepsilon )^{2}} \right] + \cdots \nonumber \\&\quad =-\frac{f_{D_s/B_s}^2m_{D_s/B_s}^4}{\pi m_{c/b}^2}\bigg \{\mathbf {Im}\frac{1}{(\omega ^2-m_{D_s/B_s}^2+i\varepsilon )^2} \nonumber \\&\qquad \times \mathbf {Re}[\mathbf {T}_{D_s/B_s}(\omega ,0)] + \mathbf {Re}\frac{1}{(\omega ^2-m_{D_s/B_s}^2+i\varepsilon )^2}\nonumber \\&\qquad \times \mathbf {Im}[\mathbf {T}_{D_s/B_s}(\omega ,0)]\bigg \}+\cdots \end{aligned}$$

(13)

$$\begin{aligned}&\quad = a \frac{d}{d\omega ^2}\delta (\omega ^{2}-m_{D_s/B_s}^2) + b \delta (\omega ^{2}-m_{D_s/B_s}^2) \nonumber \\&\qquad + c \theta (\omega ^{2}-s_{0}) . \end{aligned}$$

(14)

Here, $m_{D_s/B_s}$ and $f_{D_s/B_s}$ are the masses and decay constants of the $D_s/B_s$ mesons. In the above equation, the first term represents the double pole term and corresponds to the on shell effect of the T-matrix. The second term is the single pole term and denotes the off-shell effect of the T-matrix. The third term, proportional to c, corresponds to the continuum term and the contribution of higher states. Here the possibility of the errors may occur only through the third term of Eq. (14) and therefore special care is taken while dealing with it [83]. In this respect, the value of the continuum threshold parameter, $s_0$, is fixed so as to reproduce the vacuum masses for the $D_s$ and $B_s$ mesons. Furthermore, using Eqs. (10), (11) and (14) the shift in the masses and decay constants of $D_s/B_s$ mesons can be expressed in terms of a and b as [82, 83]

$$\begin{aligned} \delta m_{D_s/B_s} = 2\pi \frac{m_N + m_{D_s/B_s}}{m_N m_{D_s/B_s}} \rho _N a_{D_s/B_s} \end{aligned}$$

(15)

and

$$\begin{aligned}&\delta f_{D_s/B_s} \nonumber \\&\quad = \frac{m_{c/b} ^2}{2f_{D_s/B_s} m^4}\left( \frac{b \rho _N}{2m_N} - \frac{4 f_{D_s/B_s}^2 m_{D_s/B_s}^3 \delta m_{D_s/B_s}}{m_{c/b} ^2}\right) . \end{aligned}$$

(16)

Clearly, to evaluate the shift in the mass and decay constant of $D_s/B_s$ mesons we need to calculate the unknown parameters a and b.

In this respect we apply the Borel transformation on the forward scattering amplitude $T_N(\omega ,0)$ on the hadronic side using the assumption of quark hadron duality. Also, we apply the Borel transformation on the forward scattering amplitude $T_N(\omega ,0)$ calculated in operator product expansion (OPE) side in the rest frame of the nuclear matter. Then we equate these Borel transformed hadronic and OPE sides of the $T_N(\omega ,0)$ functions, and proceeding with this analysis leads to the relation between a, b and the strange quark and gluon condensates as in [82, 83]. Thus, we have

$$\begin{aligned} a E_1 + bE_2 = E_3 \end{aligned}$$

(17)

where

$$\begin{aligned} E_1 =&\left\{ \frac{1}{M^2}\exp \left( -\frac{m_{{D_s/B_s}}^2}{M^2}\right) - \frac{s_0}{m_{{D_s/B_s}}^4} \exp \left( -\frac{s_0}{M^2}\right) \right\} ,\\ E_2 =&\left\{ \exp \left( -\frac{m_{{D_s/B_s}}^2}{M^2}\right) - \frac{s_0}{m_{{D_s/B_s}}^2} \exp \left( -\frac{s_0}{M^2}\right) \right\} , \end{aligned}$$

and

$$\begin{aligned} E_3&= \frac{2m_N(m_H+m_N)}{(m_H+m_N)^2-m_{{D_s/B_s}}^2} \left( \frac{f_{{D_s/B_s}}m_{{D_s/B_s}}^2g_{{D_s/B_s}NH}}{m_{c/b}}\right) ^2\nonumber \\&\quad \times \left\{ \left[ \frac{1}{M^2}-\frac{1}{m_{{D_s/B_s}}^2-(m_H+m_N)^2}\right] \exp \left( -\frac{m_{{D_s/B_s}}^2}{M^2}\right) \right. \nonumber \\&\quad +\left. \frac{1}{(m_H+m_N)^2-m_{{D_s/B_s}}^2}\exp \left( -\frac{(m_H+m_N)^2}{M^2}\right) \right\} \nonumber \\&=-\frac{m_{c/b}\langle \bar{s}s\rangle _N}{2}\left\{ 1+\frac{\alpha _s}{\pi } \left[ 6-\frac{4m_{c/b}^2}{3M^2} \right. \right. \left. \left. -\frac{2}{3}\left( 1-\frac{m_{c/b}^2}{M^2}\right) \right. \right. \nonumber \\&\quad \times \left. \left. \log \frac{m_{c/b}^2}{\mu ^2}-2\Gamma \left( 0,\frac{m_{c/b}^2}{M^2}\right) \exp \left( \frac{m_{c/b}^2}{M^2}\right) \right] \right\} \nonumber \\&\quad \times \exp \left( - \frac{m_{c/b}^2}{M^2}\right) +\frac{1}{2}\left\{ -2\left( 1-\frac{m_{c/b}^2}{M^2}\right) \langle s^\dag i D_0s\rangle _N \right. \nonumber \\&\quad +\left. \frac{4m_{c/b} }{M^2}\left( 1-\frac{m_{c/b}^2}{2M^2}\right) \langle \bar{s} i D_0 i D_0s\rangle _N \right. \nonumber \\&\quad \left. +\frac{1}{12} \left\langle \frac{\alpha _sGG}{\pi }\right\rangle _N\right\} \times \exp \left( - \frac{m_{c/b}^2}{M^2}\right) . \end{aligned}$$

(18)

We differentiate Eq. (17) with respect to $\frac{1}{M^2}$ to find another equation:

$$\begin{aligned} a {E'_1} + bE'_2 = E'_3 \end{aligned}$$

(19)

where $E_i^{'}$ denotes the first derivative. Finally, a and b will be calculated to be $a = \frac{E_3 E_2 - E'_3 E_2}{E_1 E'_2- E'_1 E_2}$ and $b = \frac{E_3 E'_1 - E_3 E_1}{E_2 E'_1- E'_2 E_1}$.

Furthermore, the nucleon expectation values of the various condensates appearing in Eq. (18) can be calculated as [36]

$$\begin{aligned} \mathcal {O}_{N} = [ \mathcal {O}_{\rho _{B}} - \mathcal {O}_\mathrm{vacuum} ] \frac{2m_N}{\rho _B}, \end{aligned}$$

(20)

where $\mathcal {O}_{\rho _{B}}$ and $\mathcal {O}_\mathrm{vacuum}$ denote the expectation values of the operators at finite baryonic density and vacuum, respectively. Explicitly, the nucleon expectation values of strange quark and gluon condensates can be written as

$$\begin{aligned} \left\langle \bar{s}s \right\rangle _{N} = \left[ \left\langle s\bar{s} \right\rangle _{\rho _{B}} - \left\langle \bar{s}s \right\rangle _\mathrm{vacuum}\right] \frac{2m_N}{\rho _B}, \end{aligned}$$

(21)

and

$$\begin{aligned} \left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu } \right\rangle _{N}= & {} \left[ \left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu } \right\rangle _{\rho _B}\right. \nonumber \\&\left. - \left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu } \right\rangle _\mathrm{vacuum} \right] \frac{2m_N}{\rho _B},\nonumber \\ \end{aligned}$$

(22)

respectively. Also,

$$\begin{aligned} \langle \bar{s}g_s\sigma Gs\rangle _{\rho _B} = \lambda ^{2}\left\langle \bar{s}s \right\rangle _{\rho _{B}} + 3.0 \text {GeV}^{2}\rho _{B}, \end{aligned}$$

(23)

and

$$\begin{aligned} \langle \bar{s} i D_0 i D_0s\rangle _{\rho _B} + \frac{1}{8}\langle \bar{s}g_s\sigma Gs\rangle _{\rho _B} = 0.3 \ \text {GeV}^{2}\rho _{B}. \end{aligned}$$

(24)

Here we calculate the in-medium values of condensates $\left\langle \bar{s}s \right\rangle _{\rho _B}$, $\left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu } \right\rangle _{\rho _B}$ using Eqs. (6) and (7) in chiral SU(3) model. Also, we note that the effect of temperature on the shift in the masses and decay constants of the $D_s$ and $B_s$ mesons is taken through temperature dependence of the quark and gluon condensates appearing in Eqs. (6) and (7), which is further considered through the temperature dependence of the $\sigma , \zeta$ and $\chi$ fields through Eq. (5). Furthermore, using these in-medium condensates in Eqs. (23) and (24), we can calculate in-medium values of $\langle \bar{s}g_s\sigma Gs\rangle _{\rho _B}$ and $\langle \bar{s} i D_0 i D_0s\rangle _{\rho _B}$ respectively. Thus, through these in-medium condensates we can calculate the in-medium masses and decay constants of the $D_s$ and $B_s$ mesons.

4 $^3P_0$ model

We use $^3 P_0$ model to calculate the effect of the shift in the mass of $D_s(1968)$ meson on the parital decay widths of the $D_s^*(2715)$ and $D_s^*(2860)$ states decaying to ($D_s , \eta$) channel. $^3 P_0$ model was firstly invented by Micu [52], then developed for the OZI allowed decay of mesons [53,54,55,56]. In the past, the $^3 P_0$ model had been widely used for strong decays of hidden charmed states [57, 58], open charmed bottom states [59, 60], and hidden bottom [61, 62] and open bottom states [60, 63]. This assumes the creation of a quark–anti-quark pair with quantum numbers $0^{++}$. In the present work of two body decay of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons, we consider the non-relativistic transition operator [84], and arrive at the helicity amplitude given by [68]

$$\begin{aligned}&\mathcal {M}^{M_{J_A } M_{J_{B} } M_{J_C }} \nonumber \\&\quad = \gamma \sqrt{8E_A E_B E_C } \sum _{\begin{array}{c} M_{L_A } ,M_{S_A } ,M_{L_B }, \\ M_{S_B } ,M_{L_C} ,M_{S_C } ,m \end{array} }\langle {1m;1 - m}|{00} \rangle \nonumber \\&\qquad \times \langle {L_A M_{L_A } S_A M_{S_A } }| {J_A M_{J_A } }\rangle \langle L_B M_{L_B } S_B M_{S_B }|J_B M_{J_B } \rangle \nonumber \\&\qquad \times \langle L_C M_{L_C } S_C M_{S_C }|J_C M_{J_C }\rangle \times \langle \varphi _B^{13} \varphi _C^{24}|\varphi _A^{12}\varphi _0^{34} \rangle \nonumber \\&\qquad \times \langle \chi _{S_B M_{S_B }}^{13} \chi _{S_C M_{S_C } }^{24}|\chi _{S_{A} M_{S_{A} } }^{12} \chi _{1 - m}^{34}\rangle I_{M_{L_{B} } ,M_{L_C } }^{M_{L_{C}} ,m} (\mathbf K ). \end{aligned}$$

(25)

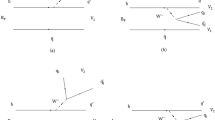
In the above, $E_{A}= m_{A}$, $E_{B} = \sqrt{m_{B}^{*2} + K_B^2}$ and $E_{C} = \sqrt{m_{C}^{*2} + K_C^2}$ represent the energies of respective mesons. Here $m^*_B$ and $m^*_C$ are the in-medium masses of the $D_s(1968)$ and $\eta$ mesons respectively. We follow the literature [68, 84], and calculate the spin matrix elements $\langle \chi _{S_B M_{S_B }}^{13} \chi _{S_C M_{S_C } }^{24}|\chi _{S_{A} M_{S_{A} } }^{12} \chi _{1 - m}^{34}\rangle$ in terms of the Wigner 9j symbol, whereas the flavour matrix element $\langle \varphi _B^{13} \varphi _C^{24}|\varphi _{A}^{12}\varphi _0^{34} \rangle$ is expressed in terms of isospin of quarks [53,54,55,56]. Furthermore, $I_{M_{L_{B} } ,M_{L_C } }^{M_{L_{C}} ,m} (\mathbf K )$ is the spatial integral for the general decay ($A \rightarrow B C$) and is written in terms of Fourier transformed harmonic oscillator meson wave function, i.e.,

$$\begin{aligned}&I_{M_{L_B } ,M_{L_C } }^{M_{L_{A} } ,m} (\mathbf {K}) = \int d \mathbf {k}_1 d \mathbf {k}_2 d \mathbf {k}_3 d \mathbf {k}_4 \delta ^3 (\mathbf {k}_1 + \mathbf {k}_2)\nonumber \\&\quad \times \delta ^3 (\mathbf {k}_3+ \mathbf {k}_4)\delta ^3 (\mathbf {k}_B- \mathbf {k}_1- \mathbf {k}_3 )\times \delta ^3 (\mathbf {k}_C - \mathbf {k}_2 -\mathbf {k}_4)\nonumber \\&\quad \times \Psi _{n_B L_B M_{L_B } }^* (\mathbf {k}_1 ,\mathbf {k}_3)\Psi _{n_C L_C M_{L_C}}^* (\mathbf {k}_2 ,\mathbf {k}_4)\nonumber \\&\quad \times \Psi _{n_{A} L_{A} M_{L_{A}}} (k_1 ,k_2 )Y _{1m}\left( \frac{\mathbf {k}_3-\mathbf {k}_4}{2}\right) , \end{aligned}$$

(26)

where $\mathbf{k}_i$ represents the momentum of corresponding quark, $\mathcal {Y}_{1}^{m}(\mathbf {k})\equiv |\mathbf {k}|^{l}Y_{l}^{m}(\theta _{k},\phi _{k})$ is the solid harmonic polynomial of the quark–anti-quark pair created in $^3 P_0$ model. By taking all these calculations in hand, we use the Jacob–Wick formula to transform the helicity amplitude into partial wave amplitude as follows:

$$\begin{aligned}&\mathcal {M}^{JL} (A \rightarrow B C) \nonumber \\&\quad = \frac{{\sqrt{2{L} + 1} }}{{2{ J_{A}} + 1}}\sum _{M_{J_B},M_{ J_C}} \langle {{ L}0{J} M_{J_{A}}} |{J_{A} M_{J_{A} } }\rangle \nonumber \\&\qquad \times \left\langle {{ J_{B}} M_{J_B} { J_C} M_{J_C}}\right| \left. {{J} M_{J_{A} } } \right\rangle M^{M_{J_{A} } M_{J_{B}} M_{J_C } } (\mathbf K ). \end{aligned}$$

(27)

In the above, $M_{J_{A}}=M_{J_B}+M_{J_C}$, $|{{J_B}}-{{J_C}}| \le {{J}} \le |{{J_B}} +{ J_C}|$ and $|{J} - {L}| \le { J_{A}} \le |{ J} + { L}|$. In the present investigation, we choose the harmonic type oscillator wave function for $D_s^*(2860) (n=1, L=2)$ and $D_s^*(2715) (n=2, L=0)$ states as [68]

$$\begin{aligned} \psi ({{\mathbf {k}_1,\mathbf {k}_2}})= & {} \frac{R^{7/2}}{\sqrt{15}\pi ^{1/4}} \mathcal {Y}_{2}^{m}\bigg (\frac{\mathbf {k}_{1}-\mathbf {k}_{2}}{2}\bigg )\nonumber \\&\times \exp \bigg [-{1\over 8}({{\mathbf {k}_1-\mathbf {k}_2})}^2R^2\bigg ], \end{aligned}$$

(28)

and

$$\begin{aligned} \psi ({{\mathbf {k}_1,\mathbf {k}_2}})&= \frac{1}{\sqrt{4\pi }}\bigg (\frac{4R^3}{\sqrt{\pi }}\bigg )^{{1}/{2}} \sqrt{\frac{2}{3}} \bigg [\frac{3}{2} - \frac{R^2}{4} ({{\mathbf {k}_1-\mathbf {k}_2})}^2 \bigg ]\nonumber \\&\quad \times \exp \bigg [-{1\over 8}({{\mathbf {k}_1-\mathbf {k}_2})}^2 R^2\bigg ]. \end{aligned}$$

Also, the harmonic oscillator wave function for the daughter mesons in ground state ($n=1$, $L=0$) will be

$$\begin{aligned} \psi ({\mathbf {k}}_1,{\mathbf {k}}_2) = \bigg (\frac{R^{2}}{\pi }\bigg )^{3/4}\exp \left( -\frac{({\mathbf {k}}_1-\mathbf{k}_2)^2}{8}R^2 \right) . \end{aligned}$$

(29)

In the above equations R denote the radius of the meson. We finally calculate the decay width, using

$$\begin{aligned} \Gamma = \pi ^2 \frac{|\mathbf{K }|}{m_{A}^2}\sum _{JL} |{\mathcal {M}^{JL}}|^2, \end{aligned}$$

(30)

where $|\mathbf K |$ is the momentum of the B and C mesons in the rest mass frame of A meson, given by

$$\begin{aligned} |\mathbf K |= \frac{{\sqrt{[m_{A}^2 - (m^*_B - m^*_C )^2 ][m_{A}^2 - (m^*_B + m^*_C )^2 ]} }}{{2m_{A} }}. \end{aligned}$$

(31)

Thus, through the in-medium mass of the $D_s(1968)$ and $\eta$ mesons, the in-medium partial decay widths of the $D_s^*(2715)$ and $D_s^*(2860)$ states decaying to ($D_s(1968), \eta$) can be calculated.

5 Results and discussion

In this section, we shall discuss the various results of the present investigation. We use parameters, nuclear saturation density, $\rho _0 = 0.15$ fm$^{-3}$, the average values of coupling constants $g_{{{D_s}N\Lambda _c}} \approx g_{{{D_s}N\Sigma _c}} \approx g_{{{B_s}N\Lambda _c}} \approx g_{{{B_s}N\Sigma _c}} \approx 6.74$, the values of continuum threshold parameter $s_0$, for $D_s$ and $B_s$ mesons, equal 7.3 and 36 GeV$^2$, respectively. We take the vacuum masses and decay constants of the $D_s ( B_s$) mesons to be 1.968 (5.37) and 0.240 (0.231) GeV, respectively [21]. Moreover, the shift in the masses and decay constants of the $D_s$ and $B_s$ mesons are represented as a function of squared Borel mass parameter, $M^2$. We choose the proper Borel window where we find the least variation in the masses and decay constants. For example, we choose the Borel windows for the masses of the $D_s$ and $B_s$ mesons as (4–6) and (28–32) GeV$^2$, respectively and, for decay constants we choose the respective Borel windows as (2–4) and (28–32) GeV$^2$. The results of the present work are very sensitive to the choice of the Borel window [35, 81,82,83]. Because of this we take different Borel windows for the masses and decay constants of the $D_s$ meson. On the other hand, for the $B_s$ meson we observe the same stable region for the shift in the mass and decay constant.

Fig. 1

The variation of the shift in the mass of pseudoscalar $D_s$ and $B_s$ mesons as a function of squared Borel mass parameter, $M^2$ for baryonic densities $\rho _0$ and $4\rho _0$. The results are given for the isospin asymmetric parameters $I = 0$ and 0.5, temperatures $T = 0$ and 100 MeV and strangeness fractions $f_s = 0$ and 0.5

Fig. 2

Figure shows the variation of the shift in decay constants of pseudoscalar $D_s$ and $B_s$ mesons as a function of squared Borel mass parameter, $M^2$ for baryonic densities $\rho _0$ and $4\rho _0$. The results are given for isospin asymmetric parameters $I = 0$ and 0.5, temperatures $T = 0$ and 100 MeV and strangeness fractions $f_s = 0$ and 0.5

5.1 Shift in the masses and decay constants

In Fig. 1 (Fig. 2) we represent the shift in masses (decay constants) of the $D_s$ and $B_s$ mesons in symmetric as well as in asymmetric hot and dense hadronic medium as a function of squared Borel mass parameter, $M^2$. In Table 1, we represent the shift in the masses and decay constants of these mesons for the baryonic densities, $\rho _0$ and 4$\rho _0$, strangeness fractions, $f_s=0$ and $f_s=0.5$, temperatures, $T=0$ and $T=100$ MeV and isospin asymmetric parameters, $I=0$ and $I=0.5$. For any particular value of temperature of the symmetric medium, we notice a drop (from vacuum values) in the masses and decay constants of the $D_s$ and $B_s$ mesons as a function of either baryonic density, $\rho _B$, or strangeness fraction, $f_s$. For example, in a symmetric nuclear medium at nuclear saturation density, $\rho _0$, and temperature $T=0$, the values of the masses and decay constants of the $D_s (B_s)$ mesons decrease by 2$\%$ (5$\%$), and 1.6$\%$ (16$\%$), respectively, from their vacuum values. Likewise, at baryonic density, 4$\rho _0$, the values of percentages drop in the masses and decay constants change to 3.3$\%$ (9.6$\%$) and 1.8$\%$ (30$\%$), respectively. On the other hand, at baryon density, $\rho _0$ and temperature $T=0$, if we move from a symmetric nuclear medium ($f_s=0$) to a symmetric strange hadronic medium ($f_s=0.5$), then the percentage drop in the masses and decay constants of the $D_s (B_s)$ mesons are observed to be 3.4$\%$ (8.4$\%$) and 3$\%$ (27$\%$), respectively, from their vacuum values. Likewise, at high baryonic density, 4$\rho _0$, the magnitude of the drop enhances to 6.5$\%$ (16$\%$) and 5$\%$ (55$\%$), respectively.

This drop of the masses and decay constants of the $D_s$ and $B_s$ mesons in the hadronic medium can be understood in terms of the in-medium dependence of the quark and gluon condensates appearing in Eq. (18). As can be seen from Eqs. (6) and (7), the scalar strange condensate $\left\langle \bar{s}s\right\rangle$ is proportional to the $\zeta$ field, and the scalar gluon condensates $\left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu }\right\rangle$, depend upon the $\sigma$, $\zeta$ and $\chi$ fields. Therefore, the behaviour of scalar fields $\sigma$, $\zeta$ and $\chi$, in the hadronic medium is reflected through the in-medium strange quark and gluon condensates and this is further reflected in the in-medium masses and decay constants of the $D_s/B_s$ mesons. As the $\zeta$ meson contains the strange quark s, this is very sensitive to the presence of hyperons in the medium. Also, we notice that the magnitude of the $\zeta$ field decreases as a function of baryonic density and strangeness fraction of the medium. Also, the dilaton field $\chi$ is observed to have a least variation in hadronic matter as compared to the scalar fields $\sigma$ and $\zeta$ [37]. For example, at finite baryonic density, 4$\rho _B$ and in zero temperature symmetric nuclear matter, the value of $\sigma$, $\zeta$ and $\chi$ fields decrease by 68$\%$, 14$\%$ and 2.9$\%$, respectively, as compared to their vacuum values. Likewise, the corresponding values of $\left\langle \bar{s}s\right\rangle$ and $\left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu }\right\rangle$ decrease by 20$\%$ and 11$\%$. On the other hand, the inclusion of hyperons along with the nucleons ($f_s=0.5$) in the symmetric hadronic matter, cause further decrease in the magnitude of $\sigma$, $\zeta$ and $\chi$ field by 68.5$\%$, 26$\%$ and 1$\%$, respectively, from their vacuum values. Likewise, the magnitude of $\left\langle \bar{s}s\right\rangle$ and $\left\langle \frac{\alpha _{s}}{\pi } {G^a}_{\mu \nu } {G^a}^{\mu \nu }\right\rangle$ decrease by 32 and 11$\%$, respectively from its vacuum values.

Therefore, this decrease in the values of the strange quark condensates and gluon condensates causes a drop in the masses and decay constants of the $D_s/B_s$ mesons.

However, we observe the opposite effect of the temperature, i.e., keeping the other parameters of medium constant, the masses and decay constants of the $D_s$ and $B_s$ mesons increase as a function of temperature of the medium. For example, at baryonic density, $4\rho _0$, temperature, $T=100$ MeV and in symmetric nuclear matter, the percentage drop in the mass and decay constant of the $D_s (B_s)$ mesons observed to be 3$\%$ (9$\%$) and 1.6$\%$ (29$\%$), respectively. Clearly, these values are slight lower than the zero temperature situations which has been mentioned earlier. The above behaviour is caused by a competing effect of the thermal distribution functions and the contributions from higher-momentum states, which further cause increase in the value of $\zeta$ field at finite temperature of the medium, as discussed in detail in Ref. [37].

Table 1 The values of the shift in the masses and decay constants of the $D_s$ and $B_s$ mesons (in units of MeV)

Fig. 3

Figure shows the contribution of individual condensates to the shift in the masses of the $D_s$ and $B_s$ mesons, in symmetric hyperonic ($f_s=0.5$) medium, at temperature $T=100$ MeV, baryonic density $\rho _B=4\rho _0$

Table 2 Contribution of individual condensates on the shift in the mass of the $D_s$ meson (in MeV) for two values of temperatures ($T=0$ and 100 MeV), strangeness fraction ($f_s=0$ and 0.5) and baryonic density ($\rho _0$ and 4$\rho _0$) in symmetric medium ($I=0$)

Furthermore, we observe that the shift in the masses and decay constants of the $D_s (B_s)$ meson is not very sensitive to the isospin asymmetric properties of the medium. As mentioned earlier, $\zeta$ contain s quark, therefore it does not change appreciably as a function of isospin asymmetry of the medium. As a result, the strange quark condensates, $\left\langle \bar{s}s\right\rangle$ do not change significantly as a function of isospin asymmetric parameter of the medium e.g., on shifting from symmetric to asymmetric nuclear medium, the magnitude of strange quark condensates, $\left\langle \bar{s}s\right\rangle$ change by 1$\%$ only, at baryonic density, 4$\rho _B$, and in zero temperature situations. Also, in the same medium conditions, the percentage change of the mass and decay constant of the $D_s (B_s)$ meson from its vacuum value is observed to be 3.3$\%$ (9.6$\%$) and 1.8$\%$ (30$\%$), respectively. Likewise, in an isospin asymmetric matter, $I=0.5$, above values change to 3.1$\%$ (9.1$\%$) and 1.6$\%$ (29$\%$), respectively.

Among the various condensates present in the QCD sum rules (Eq. (18)), the scalar strange quark condensates $\left\langle \bar{s}s\right\rangle$ has maximum contribution to the in-medium modification of the $D_s$ and $B_s$ mesons. To understand this, in Fig. 3 we plot the shift in the mass of the $D_s$ (sublot (a)) and $B_s$ (subplot (b)) mesons as a function of squared Borel mass parameter, $M^2$. We observed that, if all the condensates are set to zero, except $\left\langle \bar{s}s\right\rangle$, then the mass of the $D_s ( B_s)$ meson was observed to be 1855 (4472) MeV, and this can be compared with the mass 1840 (4461) MeV, calculated in light of all the condensates, at baryonic density $4\rho _0$, in hot and symmetric hyperonic matter. Also, we observe a negligible contribution of the other condensates to the shift in the mass of the $D_s$ meson, if we set $\left\langle \bar{s}s\right\rangle = 0$. In the present calculation, only the condensate $\left\langle s^\dag \iota D_o s \right\rangle$ is calculated in the linear density approximation at higher density. However, it follows from Fig. 3 that the contribution of $\langle s^\dag \iota D_o s \rangle$ to the shift in the masses and decay constants of $D_s/B_s$ mesons is negligible. Also, in this work, we evaluate the shift in the masses and decay constants of the $D_s/B_s$ mesons by taking the next to leading order term (NLO) to the strange quark condensates $\left\langle \bar{s}s\right\rangle$. In Table 2, we organize the numerical results of the shift in the mass of the $D_s$ meson, evaluated through a next to leading order term (NLO), and through the leading order term (LO) to $\left\langle \bar{s}s\right\rangle$. We observe the higher drop in the mass of the $D_s$ meson, evaluated using the next to leading order term, as compared to its value calculated by taking the leading order term only.

Fig. 4

We represent the variation of strange quark condensates (subplot a) and mass of the $D_s(1968)$ meson (subplot b), as a function of baryonic density, calculated in the linear density approximate QCD sum rules and compared with chiral SU(3) model, in cold symmetric nuclear medium

Here, as mentioned earlier, while deriving the Borel transformed equation for pseudoscalar $D_s$ and $B_s$ mesons, we neglected the mass of strange quark $m_s$, i.e., ($m_c+m_s) \simeq m_c$. However, if we consider the finite strange quark mass $m_s$, then we get some extra terms in the Borel transformed QCD sum rule equations $\propto m_s\left\langle \bar{s}s\right\rangle$ as discussed in [36, 74, 75]. By following this analysis, we observe an increase in the masses and decay constants of the above mentioned mesons. However, this increase is not very significant. For example, in a symmetric nuclear medium, the mass (decay constant) of the $D_s$ meson increases by 0.2 $\%$ (0.25 $\%$) only at $\rho _B=\rho _0$ and $T=0$.

Moreover, in the present work if we allow for a 10$\%$ change in the value of the coupling constant $g_{{{D_s}N\Lambda _c}} \approx g_{{{D_s}N\Sigma _c}}$, then we observe a change in the magnitude of shift in the mass of the $D_s$ meson by 2$\%$ only. However, a 10$\%$ change in the value of continuum threshold parameter $s_0$ causes a significant change of 16$\%$ in the magnitude of the shift in the mass of the $D_s$ meson. The other uncertainties of the results may be the contributions of inelastic channels in scattering processes.

Furthermore, to check the reliability of our results at the high density region, in Fig. 4, we plot the variation of strange quark condensates calculated through a linear density approximation [36], as well as using the chiral SU(3) model. In [36], using the linear density approximation, the authors calculated the strange quark condensates to be $\left\langle \bar{s}s\right\rangle = 0.8\left\langle \bar{q}q\right\rangle _{0}+ y\frac{\sigma _N \rho _B}{m_u + m_d}$, for $\sigma _N = 45$ MeV and $m_u+m_d = 11$ MeV. Here the term $\left\langle \bar{q}q\right\rangle _{0}$ is the vacuum value of the light quark condensate and is given as ($- 0.245$ GeV)$^3$. Also, the value of y was taken to be 0.5. By considering these strange condensates only, in Fig. 4 we plot the variation of the mass of the $D_s(1968)$ meson as a function of baryonic density in symmetric nuclear medium. Within the linear density approximation, we observe a linear decrease in $\left\langle \bar{s}s\right\rangle$, as well as in the mass of the $D_s$ meson as a function of baryonic density. However, the decrease in $\left\langle \bar{s}s\right\rangle$ and of the in-medium mass is non-linear, if we evaluate $\left\langle \bar{s}s\right\rangle$ using the chiral SU(3) model. A similar response was observed in the case of light quark condensates $\left\langle \bar{q}q\right\rangle$ [85]. In [85] we noticed that the non-linear behaviour of light quark condensates $\left\langle \bar{q}q\right\rangle$ calculated through the chiral SU(3) model is in accordance with the results of $\left\langle \bar{q}q\right\rangle$ calculated through loop contributions beyond the linear density approximation [86].

We now compare the results of the present investigation with the results of the other models. Using the self-consistent coupled channel approach with t-dependent vector meson exchange derived force [18, 31, 33], the authors calculated the attractive interaction of the $D_s$ meson in the hadronic matter. This is in accordance with the results of negative shift in the mass and hence favours the finite possibility of the formation of bound states of $D_s$ mesons with the nucleons as well as hyperons. The quark meson coupling model had been used in Ref. [17], and a negative mass shift of about 60 MeV was observed for the B meson, at nuclear saturation density $\rho _0$. In Ref. [87], using the heavy quark symmetry, the bound states of DN and BN states were observed with the binding energies 1.4 MeV and 9.4 MeV, respectively. As in the present work we observe an attractive interaction for $D_s$ and $B_s$ mesons in the strange hadronic medium, and similar attractive in-medium interactions were observed for D and B mesons in our previous work [85]; therefore, one might expect the observation of $D_sN$ and $B_sN$ bound states in the future PANDA experiment of the FAIR project. Recently, the chiral SU(3) model was generalized to SU(4) and was used to observe the effect of temperature, density and isospin asymmetric parameter on the in-medium masses of the $D_s$ mesons [49]. Using the chiral SU(4) model the authors observed the in-medium mass of the $D_s$ meson, 1865 (1875) MeV at temperature $T=0$ ($T=100$ MeV), and at density $\rho _B=4\rho _0$ in a symmetric nuclear medium. Likewise, in an asymmetric ($I=0.5$) nuclear medium the same values were observed to be 1875 and 1883 MeV for temperatures $T=0$ and $T=100$ MeV, respectively. However, in the asymmetric hyperonic medium, at baryonic density $4\rho _0$, because of a non-zero contribution of the Weinberg–Tomozawa term, the mass degeneracy was broken and the values of the masses of the $D_s^+$ and $D_s^-$ were observed to be 1859 and 1879 MeV, respectively.

We can compare these values with our calculated values of 1842 (1856) MeV at temperature $T=0$ ($T=100$ MeV) and baryonic density $4\rho _0$, of the symmetric nuclear medium. In [50], $B_s$ mesons in an asymmetric hyperonic medium were studied using the chiral effective approach generalized to the heavy quark sector. By using this method, in the asymmetric nuclear medium, at zero temperature, the authors observed a drop in the masses of $B_s^0$ and $\bar{B_s^0}$ mesons of nearly 67 (326) and 73 (349) MeV, respectively, at baryonic density $\rho _0$ ($4\rho _0$). As was discussed earlier, in the present work we calculate the average shift in the mass of $B_s^0 ( D_s^+)$ and $\bar{B_s^0} ( D_s^-)$ mesons by taking the averaged current density, as in Eq. (8). We can compare these results with our calculated values of the drop in the mass of the $B_s$ meson, which are 285(515) MeV at baryon density $\rho _0 ( 4\rho _0)$, for zero temperature asymmetric nuclear matter.

In [36], the masses of D / B and $D_s$ mesons were observed using the linear density approximate QCD sum rules, up to the normal nuclear density, $\rho _0$, only. Using this analysis the authors observed the $D_s-\bar{D_s}$ and $D-\bar{D}$ as well as the $B-\bar{B}$ meson mass splittings.

In [88] the authors discussed the temperature dependence of the masses, decay constants and width of heavy pseudoscalar and vector mesons. It was concluded in this work that the mass of the pseudoscalar meson varies very slow with temperature, whereas the decay constants decreases to become zero at temperature $T=T_c$. We also note this slow increase in the masses and decay constants of the $D_s$ and $B_s$ mesons as a function of temperature of the medium; this is due to fact that the scalar fields $\sigma$ and $\zeta$ first increase very slowly as a function of temperature till a value of $T \simeq 150$ MeV, and beyond this value their is an abrupt decrease[89].

Now we will discuss the possible implication of a negative shift in the mass and decay constant of the $D_s/B_s$ mesons in hadronic matter. As discussed earlier, the results of the attractive interaction of $D_s$ and $B_s$ mesons in the hyperonic (along with nucleons) medium shows the finite possibility of the observation of bound states of $D_s$ and $B_s$ mesons with nucleons as well as with hyperons. One may also expect that this drop in the mass of the $D_s ( B_s)$ meson can enhance the decay channel of various excited charmonium(bottomonium) states and these higher sates may decay to $D_s\bar{D_s}(B_s\bar{B_s})$ states instead of $J/\psi ( \Upsilon )$ states and may cause $J/\psi ( \Upsilon )$ suppression in the heavy-ion collision experiments. For the better understanding, in Fig. 5, we compare the in-medium masses of $D_s\bar{D_s}$ pairs and $B_s\bar{B_s}$ pairs with the vacuum masses of various charmonium and bottomonium states, respectively. Here, we neglect the mass modification of the charmonium and bottomonium states in the hadronic matter. It follows from Fig. 5 that the drop in the masses of the $D_s$ and $B_s$ mesons can open up the decay channel of the type $A \rightarrow D_s\bar{D_s}$ and $A \rightarrow B_s\bar{B_s}$, where A can be considered as some excited charmonium or bottomonium state. As these higher charmonium and bottomonium states are considered as a major source of $J/\psi$ and $\Upsilon$ states, the drop in the mass of the $D_s$ and $B_s$ mesons may cause these higher states to decay to the pairs of $D_s\bar{D_s}$ and $B_s\bar{B_s}$ states instead of $J/\psi$ and $\Upsilon$ states, respectively, and hence this may suppress the production of $J/\psi$ and $\Upsilon$ states in heavy-ion collision experiments. Moreover, one may also expect a decrease in the production yield of the higher charmonium and bottomonium states, and the new decay channel may cause a change in the total decay width of these higher states and this might also help in future HIC experiments to measure the total decay width of various hidden charm and bottom states.

Fig. 5

We compare the masses of the $D_s \bar{D_s}$ and $B_s \bar{B_s}$ pairs, against charmonium (subplot a) and bottomonium (subplot b) states, respectively, for different medium situations, as described in the legend

Fig. 6

The variation of partial decay widths of the $D_s^*(2715)$ mesons to a pairs of the $D_s(1968)$ and $\eta$ mesons as a function of R$_{D_s^*(2715)}$ (GeV$^{-1}$) for two values of baryonic densities ($\rho _0$ and $4\rho _0$), isospin asymmetric parameters ($I = 0$ and 0.5), temperatures ($T = 0$ and 100) MeV and strangeness fractions ($f_s = 0$ and 0.5)

Fig. 7

The variation of partial decay widths of the $D_s^*(2860)$ mesons to a pairs of the $D_s(1968)$ and $\eta$ mesons as a function of $R_{D_s^*(2860)}$ for two values of baryonic densities ($\rho _0$, $4\rho _0$), isospin asymmetric parameter ($I = 0$, 0.5), temperatures ($T = 0, 100$) MeV and strangeness fractions ($f_s = 0$, 0.5)

Furthermore, the $D_s$ and $B_s$ mesons have large leptonic and semileptonic decay widths [90]. As the masses of these mesons drop in the medium, one can also expect enhanced production of the $D_s$ and $B_s$ mesons. Therefore, as mentioned in Ref. [50], this may also cause an increase in the dilepton spectra observed in the heavy-ion collision experiments. However, if we consider the leptonic decay width of a particular $D_s$ meson, given by [91, 92]

$$\begin{aligned} \Gamma _{(D_s \rightarrow l \nu )} = \frac{G_F^2}{8\pi } f_{D_s}^{*2} |V_{cq}|^2 m_l^2 \left( 1-\frac{m_l^2}{m_{D_s}^{*2}}\right) ^2 m_{D_s}^*, \end{aligned}$$

(32)

and use medium modified values of the masses and decay constants of the $D_s$ mesons in the above equation, then we observe a decrease in the value of leptonic decay width. In Eq. (32), $G_F$ is the Fermi coupling constant, $=1.1663787 \times 10^{-5}$ GeV$^{-2}$, $m_l$ is the lepton mass, $V_{cq}$ is the CKM matrix $= 0.97$ [93], $m_{D_s}^*$ and $f_{D_s}^*$ are the in-medium mass and decay constant of the $D_s$ meson, respectively. For example, at baryonic density, $\rho _B = 4\rho _0$, in symmetric strange hadronic ($f_s=0.5$) matter, we observe the leptonic decay width of a particular channel ($D_s \rightarrow \mu \bar{\nu _\mu }$) as 5.3419 $\times 10^{-9}$ keV, which is small as compared to its vacuum value $6.3355 \times 10^{-9}$ keV. Similarly, for the leptonic decay, $D_s \rightarrow e \bar{\nu _e}$, for the same medium situations, the value of the leptonic width will be $1.2735 \times 10^{-13}$ keV and this is also small compared to its vacuum value, $1.5091 \times 10^{-13}$ keV. Therefore, we argue that the medium modification of leptonic decay widths cannot be neglected and one may also expect that the drop in the mass of the $D_s$ meson may decrease the leptonic yield in the HIC experiments. This may contradict our previously mentioned point of enhanced dilepton spectra in the HIC experiments, which is due to an enhanced production of the $D_s$ mesons. However, we argue that to understand the exact dilepton spectra, more work is required in the field of medium modification of leptonic decay widths and also on the production yield of the $D_s$ mesons in HIC experiments. To draw a definite conclusion on the temperature and density dependence of these mesons, as well as to validate the theoretical models, we seek for the possible outcomes of future experiments like CBM and PANDA, at GSI Germany.

5.2 In-medium partial decay width of the $D_s^*$(2715) and $D_s^*$(2860) mesons

In this section, using the $^3P_0$ model, we shall calculate the in-medium partial decay width of $D^*_s(2715)$ and $D_s^*(2860)$ for the processes $D_s^*(2715) \rightarrow D_s(1968) + \eta$ and $D_s^*(2860) \rightarrow D_s(1968) + \eta$, respectively (Figs. 6 and 7). The open charm states $D^*_s(2715)$ and $D_s^*(2860)$ are reported by the Belle and Babar collaborations, respectively. We consider the $D_s^*(2715)$ and $D_s^*(2860)$ states as $2 ^3S_1$ and $1 ^3D_1$ candidate [68,69,70]. As mentioned earlier, for calculating the partial decay width we shall consider the medium modified masses of daughter products only. We shall use the in-medium mass of $D_s(1968)$ meson calculated in Sect. 5.1. Additionally, we include the medium modified mass of the $\eta$ meson, calculated using heavy-baryon chiral perturbation theory combined with relativistic mean-field theory [51]. In [51] authors studied the in-medium mass of the $\eta$ mesons in symmetric nuclear matter at zero temperature including next to leading order term. Following this work, we used $- \ 75$ and $- \ 120$ MeV as values of the mass shift for $\eta$ mesons at $\rho _0$ and $4\rho _0$, respectively. As no work is yet available on the study of the mass shift of the $\eta$ mesons in asymmetric strange matter at finite temperatures, we used the same values in asymmetric strange matter as above.

In the present work, we notice a significant influence of the modification in the mass of the $D_s$ and $\eta$ mesons on the partial decay width, in addition to the respective $R_A$ values. Furthermore, we observe the enhanced in-medium values of decay widths of both the $D_s^*(2715) \rightarrow D_s(1968) + \eta$ and the $D_s^*(2860) \rightarrow D_s(1968) + \eta$ processes, as compared to their vacuum values. For example, from Figs. 6 and 7 we notice that, for any constant value of temperature, whether in symmetric ($I=0$) or in asymmetric ($I=0.5$), nuclear medium ($f_s=0$), the values of the decay widths at the nuclear matter denser medium $\rho _0$, are more than their vacuum values. Also, we observe that on increasing the density of the medium ($\rho _0 \rightarrow 4\rho _0$), decay widths further increase. This can be understood on the basis of the idea that the finite baryonic density causes a decrease in the mass of the $D_s(1968)$ and $\eta$ mesons, which further enhances the decay channel. We also observe nodes in $\Gamma _{D_s \eta } (D_s^*(2715))$ at a particular value of $R_A = 3.27$ GeV$^{-1}$. To understand the occurrence of a node we recall that on solving the spatial integral analytically for the decay process ($D_s^*(2715) \rightarrow D_s(1968) + \eta$), we get [68]

$$\begin{aligned} I^{0,0}_{0,0}=&- \sqrt{\frac{1}{2}} \frac{|\mathbf {k}_{B}| \pi ^{1/4}R_{A}^{3/2}R_{B}^{3/2}R_{C}^{3/2}}{(R_{A}^{2}+R_{B}^{2}+R_{C}^{2})^{5/2}} \nonumber \\&\quad \{ -6(R_{A}^{2}+R_{B}^{2}+R_{C}^{2})(1+\xi )+R_A^2 [ 4+20\xi \nonumber \\&\quad +\mathbf {k}_{B}^2 (R_{A}^{2}+R_{B}^{2}+R_{C}^{2}) (-1+\xi )^2(1+\xi ) ] \}\nonumber \\&\quad \times \exp \bigg [-\frac{\mathbf {k}_{B}^{2}R_{A}^{2}(R_{B}^{2}+R_{C}^{2})}{8(R_{A}^{2}+R_{B}^{2}+R_{C}^{2})}\bigg ]. \end{aligned}$$

(33)

Fig. 8

Variation of partial decay width of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons as a function of respective $R_A$ values with and without including the medium modified masses of $D_s^*(2715)$ and $D_s^*(2860)$ mesons

In the above, the polynomial part written within braces becomes zero as the value of $R_{D_s^*(2715)}$ approaches 3.27 GeV$^{-1}$ and thus, nodes are observed in $\Gamma _{D_s \eta } (D_s^*(2715))$ at this value of $R_A$. This happens because of the nodal structure of the simple harmonic oscillator wave function of the first excited state $1^-(2^3 S_1)$ of the parent meson. Furthermore, as the masses of $D_s(1968)/\eta$ mesons contribute through the momentum $\mathbf{K} = \mathbf{k_B}$, given by Eq. (31) and it is present in the polynomial part of Eq. (33), and therefore, the modification in the masses of the $D_s(1968)$ and $\eta$ mesons have finite (though small) effect on the position of node. It is clear from Eq. (31) that the decrease in the masses of the $D_s(1968)/\eta$ mesons cause increase in the value of momentum $\mathbf{K}$. This increase in the value of momentum $\mathbf{K}$, further change the position of node e.g., at zero temperature, for baryonic density $\rho _B = 4\rho _0$, $\eta = 0.5$ and $f_s = 0.5$, the position of node shift to $R_A = 3.07$ GeV$^{-1}$, compared to the original value $R_A=3.27$ GeV$^{-1}$. On the other hand, we do not observe nodes in the decay process, $D_s^*(2860) \rightarrow {D_s(1968) + \eta }$, and this is because of the state $1^3 D_1$ of the parent meson. Furthermore, for any constant value of baryonic density, isospin asymmetric parameter and temperature of the medium, we observe an enhancement in the decay width as we move from nuclear ($f_s=0$) to hyperonic medium ($f_s=0.5$). As explained in Sect. 5.1, the mass of the $D_s$ meson decrease further in the strange medium ($f_s=0.5$), and this further cause increase in the possibility of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons decaying to channel ($D_s(1968)$ $\eta$). On the other hand, as mentioned in Sect. 5.1, finite temperature causes an increase in the mass of the $D_s(1968)$ meson and this further causes decrease in the decay width of the above mentioned processes. Talking about the isospin asymmetric parameter, as discussed earlier, the strange quark condensate is not very sensitive to the isospin asymmetry of the medium. Therefore, we could not observe much significant effect of isospin asymmetry on both the values of $\Gamma _{D_s \eta } (D_s^*(2715))$ and of $\Gamma _{D_s \eta } (D_s^*(2860))$, in nuclear medium. However, in cold ($T=0$) hyperonic medium ($f_s=0.5$), and four times the nuclear matter density ($4\rho _0$), we observe a slight increase in the decay width of the above mentioned decay processes, as is clear from Figs. 6 and 7. This is due to decrease in the mass of $D_s(1968)$ meson in asymmetric hyperonic matter (mentioned in Sect. 5.1). Now to compare the results, as far as our knowledge about the literature is concerned, in-medium decay width of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons have not been studied, however, many authors have predicted their spectroscopy and calculated their decay widths in vacuum using microscopic $^3P_0$ model [59, 64, 65, 68, 69, 94]. Apart from $^3P_0$ model other models like quark model including quark meson effective Lagrangian approach and heavy quark effective theories had also been applied to investigate the decay widths of excited $D_s$ mesons [66, 67]. Here in the present work, we take a non-relativistic transition operator to calculate the partial decay width of the above mentioned mesons [52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67]. However, if we consider a relativistic approach to formulate $^3P_0$ model as mentioned in [95], then there will be interaction Hamiltonian containing Dirac quark fields, $H_I = g \int _{a}^{b} d^3x \bar{\psi } \psi$, for g = 2$\gamma m_s$. We fix the value of coupling constant g through the original value of quark pair creation strength parameter $\gamma = 6.4$. Now considering relativistic correction to the mass of strange quark $m_s$, if we increase its value by 5$\%$, then we observe a decrease in the partial decay width of $\Gamma _{D_s \eta } (D_s^*(2715)) \ ( \Gamma _{D_s \eta } (D_s^*(2860)))$ by 10$\%$ (5$\%$), to its original values in symmetric matter at baryon density $\rho _0$ and temperature $T = 0$.

In the above discussion of in-medium partial decay width, we neglected the mass modification of parent $D_s^*(2715)$ and $D_s^*(2860)$ mesons. To the best of our knowledge, no work is available with an in-medium study of the masses of these parent mesons. However, in order to understand the effect of medium modified masses of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons on their partial decay width, we recall the in-medium study of the ground state strange vector mesons $D_s^*$ and $B_s^*$ [37]. In Ref. [37], in symmetric nuclear medium, at $\rho _B=\rho _0$ and $T = 0$, we observed a decrease in the values of the masses of the $D_s^*$ and $B_s^*$ mesons by 2.3 and 3.7$\%$, respectively, from their vacuum values. Likewise at higher baryonic density $4\rho _0$, medium mass of the above mentioned mesons further decrease to 3.7 and 6.8$\%$, respectively from their vacuum values. From this experience of the medium modification of the ground state vector $c\bar{s}$ and $\bar{b}s$ states, we also expect a similar kind of drop in the masses of excited $c\bar{s}$ states. Here it should be noted that, as a function of baryonic density, the in-medium mass of $D^*_s$ meson decreases very fast till baryonic density $\rho _B \simeq 1.5\rho _0$, and beyond that this decrease become slow. This behaviour can be understood on the basis of the in-medium behaviour of light quark and gluon condensates, which further depend on the in-medium behaviour of $\sigma$, $\zeta$ and $\chi$ fields (discussed in previous section). The decrease in the values of $\sigma$ and $\zeta$ fields as a function of baryonic density is very fast till the baryonic density $\rho _B \simeq 1.5\rho _0$ and beyond that the decrease become slow. From this we expect a decrease in the mass of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons at baryonic density $\rho _0 (4 \rho _0)$ of approximately 3$\%$ (5$\%$). In Fig. 8, we present the effect of medium modified masses of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons on their partial decay widths. We observe that the inclusion of the medium modified masses of these parent mesons further decrease the value of the partial decay width. For example, if we allow 3$\%$ decrease in the masses of the $D_s^*(2715)$ and $D_s^*(2860)$ mesons, in symmetric nuclear medium, at $\rho _B = \rho _0$ and $T = 0$, then the values of $\Gamma _{D_s \eta } (D_s^*(2715))$ and $\Gamma _{D_s \eta } (D_s^*(2860))$ are observed to be 8 and 17.2 MeV, respectively. Likewise, expecting 5$\%$ drop in the mass of the parent mesons $\rho _B = 4\rho _0$, we observed partial decay widths as 7.6 and 16.2 MeV, respectively. Clearly, these values are less than the respective values of $\Gamma _{D_s \eta } (D_s^*(2715))$ and $\Gamma _{D_s \eta }(D_s^*(2860))$ observed without modifying the mass of parent mesons, i.e., 12 and 30 MeV (13 and 32 MeV), in symmetric matter at baryon density $\rho _0$ ($4\rho _0$) and temperature $T = 0$. Expecting a larger shift in the mass of excited $D_s^*$ mesons, say, 6$\%$ at $\rho _0$, and 10$\%$ at $4\rho _0$, we observed a further decrease in the values of the partial decay width.

A more detailed study of the masses of $D_s^*(2715)$ and $D_s^*(2860)$ mesons in asymmetric strange hadronic medium and its possible implication on the in-medium decay width of the processes discussed above will be a goal of future study.

6 Summary

We observed the negative shift in the masses and decay constants of the pseudoscalar $D_s(1968)$ and $B_s(5370)$ mesons, using the chiral SU(3) model and the QCD sum rules technique. Furthermore, we take the in-medium mass of the $D_s(1968)$ meson as an application in $^3P_0$ model and observe the in-medium partial decay widths of excited $c\bar{s}$ states, i.e., $D_s^*(2715)$ and $D_s^*(2860)$ mesons decaying to $D_s(1968)+\eta$. We observe that, as the mass of the $D_s(1968)$ meson decreases in the hyperonic (along with the nucleons) medium, this results in the significant increase in the corresponding partial decay widths. In the present paper, we have neglected the modification in the masses of the parent mesons $D_s^*(2715)$ and $D_s^*(2860)$. We emphasise the fact that, even at the higher density region, the above calculated in-medium decay width never seems to be more than the vacuum decay width of the $D_s^*(2715)/D_s^*(2860)$ to the channel DK. In the future it will be of interest to include the other decay channel in the calculations to evaluate the in-medium decay width.